LISTA DE CONTEÚDO
- INTRODUÇÃO
- SEGMENTOS ORIENTADOS
- VETORES
- ADIÇÃO DE VETORES (E LEI DOS COSSENOS)
- SUBTRAÇÃO DE VETORES
- PROPRIEDADES DOS VETORES (E LEI DOS SENOS)
- MULTIPLICAÇÃO POR ESCALAR
- VETOR UNITÁRIO
- SISTEMA CARTESIANO DE COORDENADAS
- DISTÂNCIA PONTO À PONTO
- EQUAÇÃO DA CIRCUNFERÊNCIA E DA ESFERA
- EQUAÇÃO VETORIAL DA RETA
- EQUAÇÃO VETORIAL DO PLANO
- SISTEMA CILÍNDRICO DE COORDENADAS
- SISTEMA ESFÉRICO DE COORDENADAS
- CENTRO DE MASSA
- DEMONSTRAÇÃO DA LEI DOS COSSENOS
- DEMONSTRAÇÃO DA LEI DOS SENOS
- BIBLIOGRAFIA
INTRODUÇÃO
Antes mesmo de começarmos a falar de conceitos físicos somo velocidade, aceleração e deslocamento, vamos falar de uma ferramenta muito útil para tratar destes conceitos em problemas de mais de uma dimensão.
Isto é, vamos falar dos Vetores.
Os vetores são bastante utilizados não só na física, mas também na matemática (geometria analítica, cálculo vetorial, etc) e em outras áreas que utilizam a física e a matemática como ferramental para tratar de problemas reais. Podemos citar as engenharias como um todo e a área de programação de computadores entre muitas outras.
Vamos começar então dando um conceito matemático sobre o que é vetor. Iniciarei dando um conceito bastante abstrato, mas a ideia é que você aplique este conceito em problemas que irá enfrentar no futuro. Espero que assim você entenda melhor o porque da chamada "regra do paralelogramo" e outras operações comuns.
Primeiramente se faz necessário especificar qual a notação que usaremos:
Vou seguir esta notação.
Para começar, imagine dois pontos no espaço.
Sobre estes dois pontos podemos traçar um segmento de reta (com extremidades em P e Q) o qual chamaremos de "segmento PQ"; podemos traçar uma "reta PQ", cuja diferença entre segmento de reta e reta é que esta última não possui fim nem começo (os três pontinhos no final da figura abaixo representa isto).
Podemos adicionar um terceiro ponto R. Existe apenas um plano distinto que contém todos os três pontos (pois eles não são colineares. Por exemplo, pegue três pontos quaisquer da reta PQ e verifique que existem infinitos planos que os contém), com isso podemos falar em "plano PQR"
SEGMENTOS ORIENTADOS
Você deve estar se perguntando porque estou falando de segmento, fazendo isto parecer mais uma aula de matemática. Bom, o motivo é que vetores é um conceito matemático que é aplicado na física. Você deve se lembrar que no final da aula dois (link ao lado: 2. Unidades de Medidas), no final, há uma breve discussão sobre grandezas vetoriais e escalares. Então voltaremos a isto.
Alguns exemplos de grandezas escalares são: área (ex. um apartamento de 50 m$^{2}$), comprimento (ex. uma barra de comprimento 4 m; não confunda com vetor deslocamento), massa (ex. uma pessoa de 78 kg). Todas estas grandezas tem algo em comum: não possuem direção nem sentido! Por exemplo: seja uma pessoa que possui 78 kg; não há significado algum perguntar "qual a direção de sua massa?" ou afirmar que "certa pessoa possui 78 kg para a direita. Estas grandezas serão estudadas posteriormente.
Vamos então nos focar em grandezas vetoriais tais como velocidade vetorial (ex. um veículo dirigindo-se para o norte com velocidade de 50 km/h), força (ex. uma pessoa de 78 kg sobre uma balança, empurra a balança para baixo com uma força de 780 N), entre outras grandezas que tem significado afirmações como "na direção horizontal", "com sentido da direita para a esquerda", etc.
Acima dois exemplos de vetores, sendo que o vetor força ($\overrightarrow{F} $) apresenta o ângulo formado com a horizontal e o vetor velocidade ($\overrightarrow{V} $) apresenta duas de suas componentes. Aqui não demos importância para o tamanho do corpo que sofre a força ou que possui determinada velocidade.
Imagine agora que você queira determinara a velodidade de um corpo rígido sem rotação, apenas translação. Qual seria a velocidade do corpo?
Aqui uma propriedade importante dos vetores: o vetor velocidade do corpo rígido é o conjunto de TODOS os segmentos orientados (setas no desenho). Isso mesmo, TODOS! Acontece que existem infinitos segmentos orientados, pois podemos escolher um para cada ponto no corpo, por isso podemos escolher apenas um deles. Essa propriedade é importante e acredito que deixará mais clara algumas operações com vetores que faremos futuramente.
Vamos então definir o que é Segmento Orientado.
Voltemos aos pontos P e Q acima. Nós podemos escolher uma direção e sentido para seguir, por exemplo, digamos que temos o segmento orientado PQ. Podemos escolher sair do ponto P e ir para o ponto Q e a isso damos o nome de segmento orientado PQ.
Podemos escolher outros dois pontos AB tais que o segmento de reta AB seja paralelo ao segmento de reta PQ. Assim podemos definir outro segmento orientado AB (Veja figura abaixo). Continuando com esta ideia, podemos escolher outros dois pontos CD e definir outro segmento orientado, porém agora um com origem em D e destino em C e chamamos de segmento orientado DC.
É importante observar que:
Algumas propriedades de equipolência:
VETORES
Vamos agora definir então o que é vetor:
Observe que o vetor $\overrightarrow{AB}$ possui sentido oposto ao vetor $\overrightarrow{BA}$, assim dizemos que $\overrightarrow{BA} = -\overrightarrow{AB}$ ou, se dissermos que $\overrightarrow{x} = \overrightarrow{AB}$, então $\overrightarrow{x} = -\overrightarrow{BA}$ ou mesmo que $-\overrightarrow{x} = \overrightarrow{BA}$.
ADIÇÃO DE VETORES
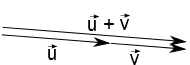
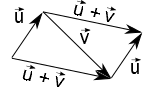
Sejam três pontos não colineares A, B e C. Diremos que o segmento orientado AB é um elemento do conjunto (vetor) $\overrightarrow{u}$ e que o segmento orientado CD é um elemento do conjunto $\overrightarrow{v}$. Por definição o vetor soma é o conjunto que contém o segmento orientado AC. Veja figura a seguir.
De forma equivalente, temos três pontos A', B', C' tais que o seguimento orientado A'B' é equipolente à AB, B'C' equipolente à BC e, consequentemente, A'C' equipolente à AC. Assim, temos dois triângulos congruentes (semelhantes e com as mesmas dimensões) o que nos permite representar os vetores $\overrightarrow{u}$, $\overrightarrow{v}$ e $\overrightarrow{u} + \overrightarrow{v}$ em outros locais do espaço.
Se ambos os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ tiverem a mesma origem, surge a conhecida "regra do paralelogramo":
Observe que o segmento de reta AB é paralelo à CD, AC à BD e portanto o segmento orientado AB é equipolente à CD e AC à BD, assim podemos "mudar" os vetores de lugar e chegar na definição de soma de vetores.
Matematicamente, se você souber os módulos de dois vetores que se deseja somar, pode-se obter o módulo do vetor soma $\vec{u} + \vec{v}$ utilizando-se da lei dos co-senos.
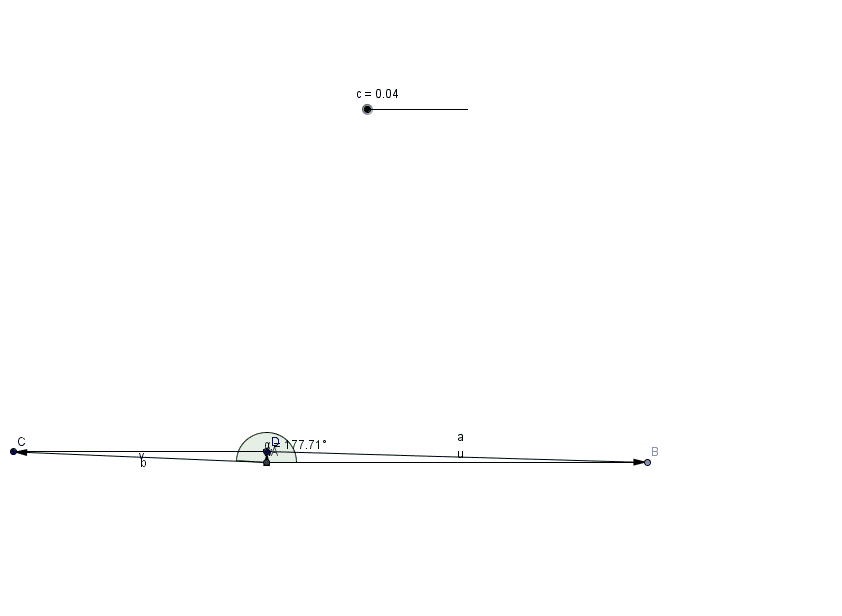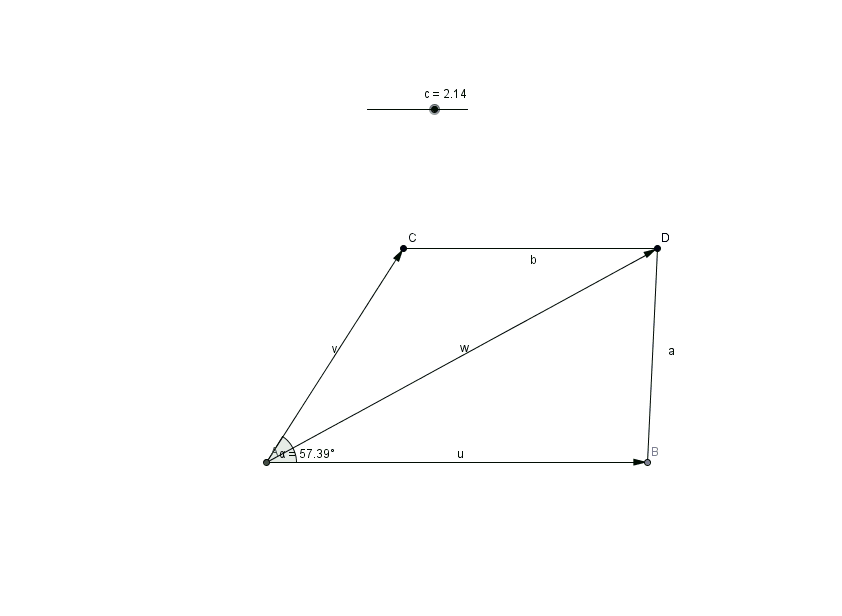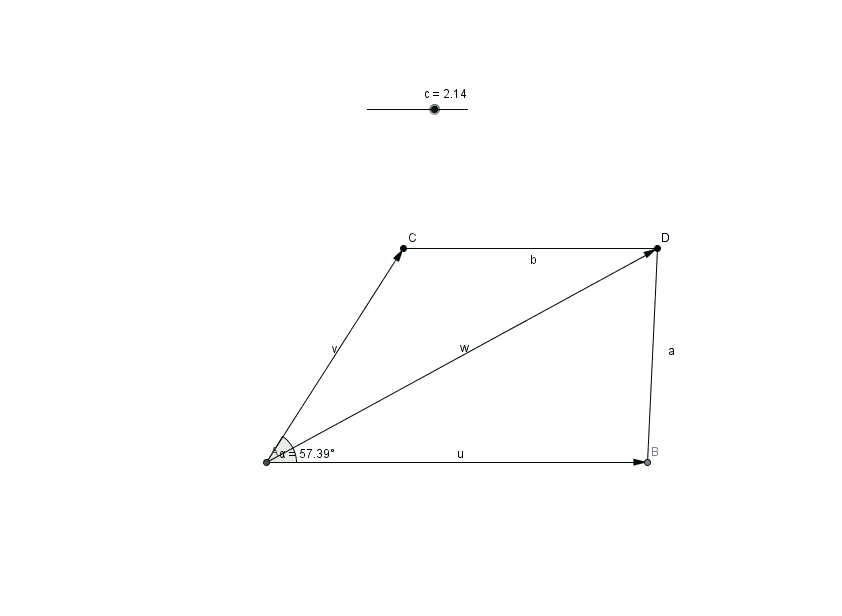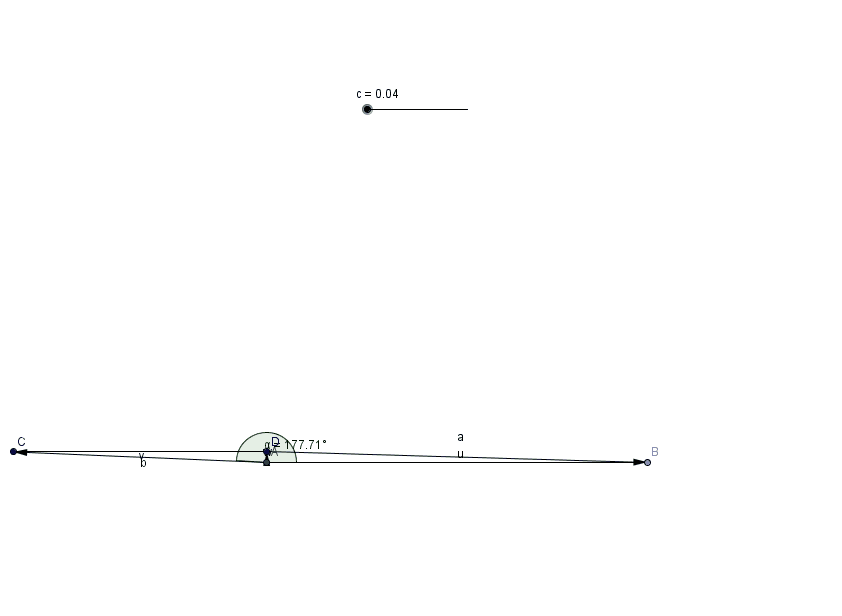
Escolhendo outro elemento do conjunto $\vec{v}$, podemos encontrar o vetor resultante. Observe na figura abaixo que os ângulos $\alpha$ e $\beta$ são suplementares, isto é, $\alpha + \beta = 180°$.
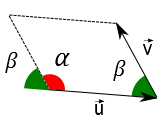
Observe agora a figura abaixo. Nela formamos um triângulo cujos lados possuem tamanhos iguais aos módulos dos vetores $\vec{u}$, $\vec{v}$ e $\vec{u} + \vec{v}$. Se estiver lembrando-se da matemática que a lei dos cossenos é:
$$s^2 = u^2 + v^2 - 2uv \cos{\beta}$$
podemos então reescrever esta lei para a Física. Observe que aqui $s^2 = |\vec{u} + \vec{v}|^2$ é o "tamanho" do lado oposto ao ângulo $\beta$ do triângulo formado pelos vetores, conforme figura a seguir.
Primeiramente, observe que partimos do ângulo formado entre os dois vetores $\vec{u}$ e $\vec{v}$ quando ambos possuem origem em comum. Assim vamos tentar reescrever a lei dos cossenos porém em função de $\alpha$.
Talvez você se lembre que, dados dois ângulos suplementares $\alpha$ e $\beta$ (que somados formam 180°), então $\cos{\alpha}=-\cos{\beta}$, assim basta substituir $\cos{beta}$ na equação da lei dos cossenos vista anteriormente por $-\cos{\alpha}$, obtendo-se:
$$s^2 = u^2 + v^2 + 2uv \cos{\alpha}$$
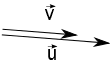
Vamos observar aqui alguns casos particulares para valores de $\alpha$ e, consequentemente, para valores de $\beta$.
$$s^2 = u^2 + v^2 + 2uv \cos{\alpha}$$ $$s^2 = u^2 + v^2 + 2uv \cos{0}$$ $$s^2 = u^2 + v^2 + 2uv \cdot 1$$ $$s^2 = u^2 + v^2 + 2uv$$ $$s^2 = u^2 + 2uv + v^2$$ $$s^2 = (u + v)^2$$ $$s = \sqrt{(u + v)^2}$$ como $u>0$ e $v>0$, então $\sqrt{(u + v)^2}=|u + v|=u + v$, ou seja, $$s = (u + v)$$ Observe a figura a serguir para entender o que está acontecendo:
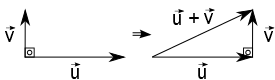
Se usarmos a definição geométrica de soma de vetores para este caso, obtemos:
$$s^2 = u^2 + v^2 + 2uv \cos{\alpha}$$ $$s^2 = u^2 + v^2 + 2uv \cos{90°}$$ $$s^2 = u^2 + v^2 + 2uv \cdot 0$$ $$s^2 = u^2 + v^2 + 0$$ $$s^2 = u^2 + v^2 $$ Para um bom observador esta equação não é nada mais nada menos do que o Teorema de Pitágoras. Veja a figura a seguir:
$$s^2 = u^2 + v^2 + 2uv \cos{\alpha}$$ $$s^2 = u^2 + v^2 + 2uv \cos{180°}$$ $$s^2 = u^2 + v^2 + 2uv \cdot (-1)$$ $$s^2 = u^2 + v^2 - 2uv$$ $$s^2 = u^2 - 2uv + v^2$$ $$s^2 = (u - v)^2$$ $$s = \sqrt{(u - v)^2}$$ como $u>0$ e $v>0$, porém não necessariamente $u - v > 0$ então $\sqrt{(u - v)^2}=|u - v|$, ou seja, $$s = |u - v|$$ Observe a figura a serguir:
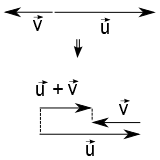
Abaixo uma pequena animação da soma de dois vetores. Neste caso, o vetor $\vec{u}$ permanece com módulo, direção e sentido inalterados; o vetor $\vec{v}$ mantém apenas o seu módulo constante; e o vetor soma $\vec{w} = \vec{u} + \vec{v}$ varia o seu módulo, direção e sentido. Consideremos o ângulo $\alpha$ variando.
Vale apena observar que aqui estou usando o símbolo $|x|$ para representar o valor absoluto (módulo) de um número real $x$ e também para expressar o tamanho (também chamado de módulo) de um vetor $|\vec{x}|$. Em ambas as situações, obtemos um número positivo (ou seja, maior ou igual à zero). Eis aqui mais um pequeno rigor: chamaremos de números:
Aqui, a frase $\forall x \in \mathbb{R} | x\geq 0$, pode ser lida como: "para todo x pertencente aos reais tal que x maior ou igual à zero". Ou seja, alguns simbolos resume paravras ou frases: $\forall=$ "para todo"; $\in =$ "pertencente à"; $\mathbb{R}=$ "conjunto dos números reais"; e $|=$ "tal que". Guardem estes símbolos, pois lhes serão úteis futuramente.
SUBTRAÇÃO DE VETORES
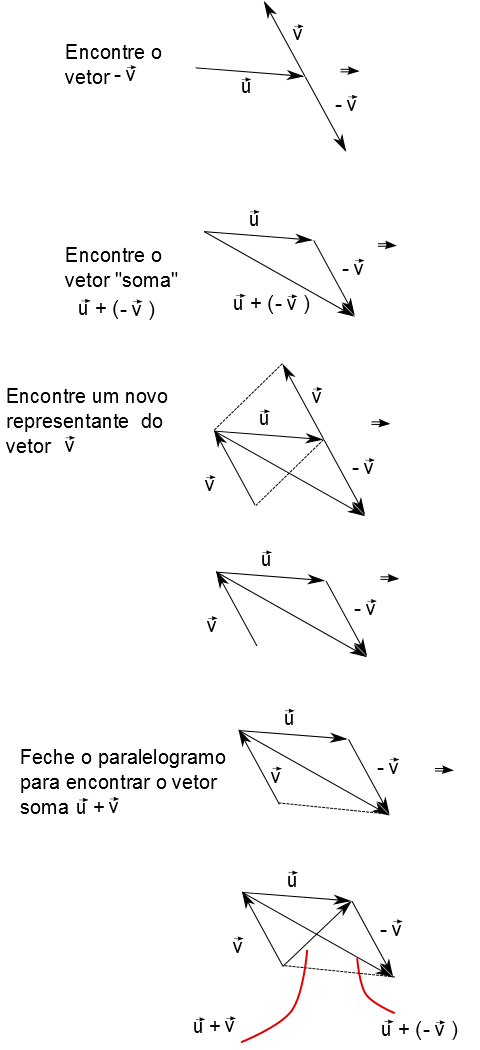
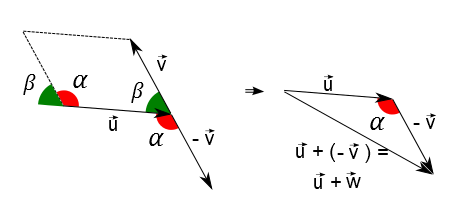
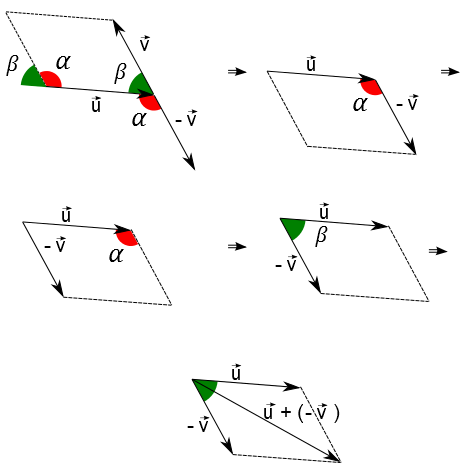
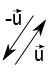
Geometricamente, a subtração de vetores se faz invertendo o sentido do vetor que se deseja subtrair. Como exemplo, peguemos os vetores $\vec{u}$ e $\vec{v}$. Agora, vamos encontrar o vetor diferênça $\vec{u}-\vec{v}$.
Primeiramente escrevemos $$\vec{u}-\vec{v}=\vec{u}+(-\vec{v})$$ sendo que o vetor $-\vec{v}$ é o $\vec{v}$ com sentido invertido. Ou seja, como já vimos como fazer a soma de dois vetores, então procede-se como já foi visto anteriormente (para soma de vetores): $\vec{u}+(-\vec{v})$
Vamos lá: primeiro você encontra o vetor $-\vec{v}$:

Depois efetua-se a soma como feito pela definição geométrica da soma:
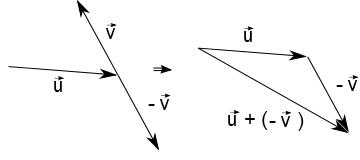
Pronto! Encontrado geometricamente o vetor soma!
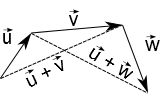
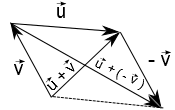
A figura a seguir apresenta uma propriedade do paralelogramo formado pela "regra do paralelogramo". A propriedade nos diz que uma das diagonais do paralelogramo é o vetor soma enquanto que a outra diagonal é o vetor diferença:
Para finalizar, observe que a lei dos cossenos troca de sinal! Como assim? Bom, vamos dizer que um outro vetor $\vec{w} = -\vec{v}$ e procedendo como feito anteriormente para a lei dos cossenos:
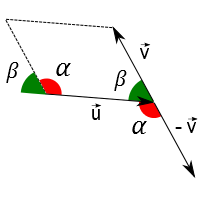
Observe a figura acima. Suponha que tenha sido dado o ângulo $\alpha$ entre os vetores $\vec{u}$ e $\vec{v}$ (cuidado, pois não é entre $\vec{u}$ e $-\vec{v}$). A lei dos cossenos usual da matemática fica somo se segue: $$|\vec{u}-\vec{v}|^2 = u^2 + v^2 - 2uv \cos{\alpha}$$
Compare com o vetor soma: $$|\vec{u}+\vec{v}|^2 = u^2 + v^2 + 2uv \cos{\alpha}$$
Se penssarmos na lei dos cossenos usual da física, teríamos: $$|\vec{u}-\vec{v}|^2 = u^2 + v^2 + 2uv \cos{\beta}$$ Compare com o vetor soma: $$|\vec{u}+\vec{v}|^2 = u^2 + v^2 - 2uv \cos{\beta}$$
Para mais clareza, veja figura a seguir:
É importante compreender bem as equações a seguir para não confundir os sinais. Eu disse compreender e não decorar. Se tentar decorar simplesmente, irá confundir em exercícios futuros, mas se entender, saberá aplicar com mais clareza estas equações. De forma simplificada, pense que o sinal de "menos" antes do cosseno surge na lei dos cossenos pensando no que você verá na matemática, isto é, pensando no ângulo formado entre os vetores $\vec{u}$ e $\vec{v}$ quando estes formam, junto com o vetor soma, um triângulo. Os demais casos surgem como consequência trigonométrica e geométrica do problema.
A seguir você verá algumas propriedades dos vetores. Você irá ver que subtrair o vetor $\vec{v}$ de um outro vetor qualquer é um caso particular de multiplicação de um vetor por um escalar (isto é, por um número) igual à -1. Você verá que se o escalar for negativo, então o vetor mudar de sentido, por isso nós somamos o vetor $\vec{u}$ ao vetor $-\vec{v}$.
PROPRIEDADES DOS VETORES
Agora que temos uma definição mais formal sobre o que é um vetor - isto é, um conjunto de infinitos segmentos orientados equipolentes - podemos então estudar e entender algumas propriedades dos vetores. Vamos começar com propriedades relacionadas à soma:
- Propriedade Associativa
- Propriedade Comutativa
- Propriedade da existência do Elemento Neutro
- Propriedade da existência do Elemento Oposto
Pode-se efetuar a soma de três ou mais vetores na ordem em que você preferir. Por exemplo, para o caso da soma de três vetores $\vec{u}$, $\vec{v}$ e $\vec{w}$, você pode somar os dois primeiros e depoir os dois últimos ou somar o primeiro ao vetor soma dos outros dois.
A equação abaixo expressa isso. Observe que o que está entre parênteses é uma operação que deve ser efetuada antes.
$$(\vec{u} + \vec{v})+ \vec{w} = \vec{u} + (\vec{v} + \vec{w})$$
Obserev a figura abaixo, pois ela representa esta propriedade.
$$\vec{u} + \vec{v} = \vec{v} + \vec{u}$$
$$\vec{u} + \vec{0} = \vec{v}$$
Chamaremos o conjunto $\vec{0}$ de elemento neutro ou vetor nulo. Você pode escolher um segmento orientado deste conjunto que o representa. Consegue pensar em algum? Na verdade, qualquer segmento orientado no qual o ponto inicial e final são coincidentes, assim fica razoável esta propriedade se você utilizar da definição geométrica de soma de vetor.
Este vetor também pode ser representado por: $\vec{0} = \vec{AA}$ è importante observar que um vetor nulo é, por definição, paralelo à qualquer outro vetor.
Existe um elemento oposto à qualquer vetor $\vec{u}$ tal que, somado ao vetor $\vec{u}$, tem-se como resultado o vetor nulo $\vec{0}$. Este elemento é simbolizado por $-\vec{u}$. Assim:
$$\vec{u} +(-\vec{u}) = \vec{AB} + \vec{BA} = \vec{AA} = \vec{0}$$
Com esta propriedade podemos subtrair vetores e obter a propriedades das diagonais do paralelogramo:
Lei dos senos para os vetores
Talvez você se lembre da lei dos senos na matemática.
Observer a figura abaixo. Nela temos um triângulo com os respectivos ângulos internos.
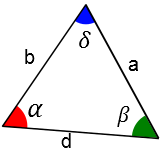
A lei dos senos nos da a seguinte relação entre os ângulos internos de um triângulo e seus lados:
$$\frac{\rm{a}}{\rm{sen}{\alpha}} = \frac{b}{\rm{sen}{\beta}} = \frac{d}{\rm{sen}{\delta}}$$
Vamos substituir os lados seste triângulo por vetores. Ao fazer isso pode-se verificar que a soma dos três vetores será nula: $$\vec{u} + \vec{v} + \vec{w} = \vec{0}$$
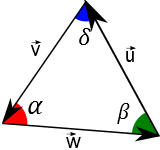
E a lei dos senos na matemática se mantém, bastando substituir os lados dos triângulos pelos módulos dos vetores que os compõem. Ou seja:$$\frac{|\vec{u}|}{\rm{sen}{\alpha}} = \frac{|\vec{v}|}{\rm{sen}{\beta}} = \frac{|\vec{w}|}{\rm{sen}{\delta}}$$
Mas se colocarmos os vetores todos com uma origem em comum, obtemos novamente a equação acima. Para verificar isso, observe o desenho a seguir.
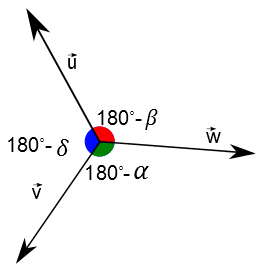
Lembrando que $\rm{sen}(180^o - \alpha) = \rm{sen{\alpha}}$, podemos manter todos os denominadores na lei dos senos e substituir os numeradores pelos respectivos módulos dos lados dos triângulos: $$\frac{|\vec{u}|}{\rm{sen}{\alpha}} = \frac{|\vec{v}|}{\rm{sen}{\beta}} = \frac{|\vec{w}|}{\rm{sen}{\delta}}$$
MULTIPLICAÇÃO POR ESCALAR
Vamos agora ver as propriedades de multiplicação de um vetor por um escalar.
A multiplicação de um vetor por um escalar (um número real, i.e., pode ser negativo, nulo, inteiro, irracional como o $\pi$, etc) tem como propriedade alterar apenas o módulo e o sentido de um vetor, sendo incapaz de mudar sua direção.
Temos então as seguintes propriedades:
Seja $\alpha \in \Re$ e um vetor $\vec{v} \in V^3$ (isto é, ao espaço formado por todos os vetores tridimensionais), então $\alpha \vec{v}$ é a expressão que representa a multiplicação do vetor $\vec{v}$ pelo escalar $\alpha$.
Se $\alpha = 0$ ou $\vec{v} = \vec{0} \Rightarrow \alpha \vec{v} = \vec{0}$ (por definição).
Se $\alpha \neq 0$ e $\vec{v} \neq \vec{0} $ então:
a) $\alpha \vec{v}$ é paralelo à $\vec{v}$
b)$\alpha \vec{v}$ e $\vec{v}$ possuem mesmo sentido se $\alpha > 0$ e possuem sentido oposto se $\alpha < 0$
c)$|\alpha \vec{v}| = |\alpha| \cdot |\vec{v}|$
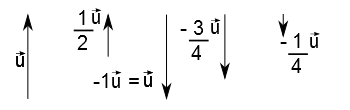
- Propriedade Distributiva 1
$$\alpha (\vec{u} + \vec{v}) = \alpha \vec{u} + \alpha \vec{v} $$
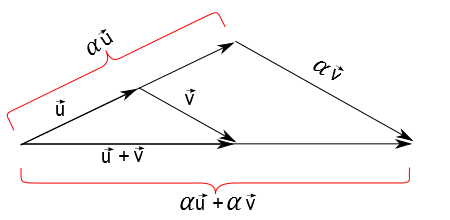
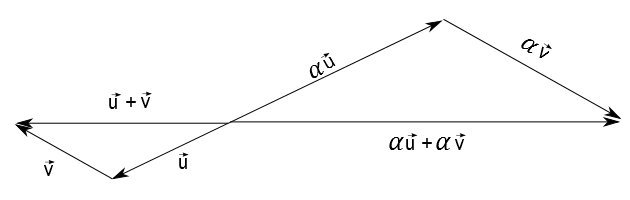
A figura acima representa esta propriedade para o caso em que $\alpha > 0$ e a figura abaixo para o caso em que $\alpha < 0$
- Propriedade Distributiva 2
$$(\alpha + \beta) \vec{u} = \alpha \vec{u} + \beta \vec{u}$$
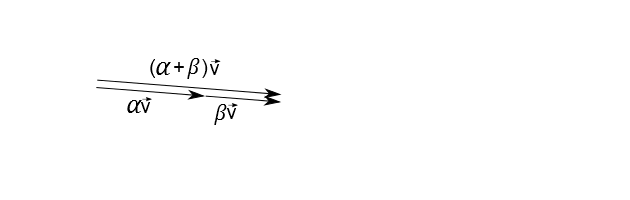
- Propriedade da existência do Elemento Neutro
$$1 \cdot \vec{v} = \vec{v}$$
- Propriedade Associativa
$$(\alpha \beta) \vec{v} = \alpha (\beta \vec{v}) = \beta (\alpha \vec{v})$$
VETOR UNITÁRIO
Vamos agora introduzir o conceito de vetor unitário, uma vez que será útil sempre que fizermos a decomposição de vetores, como será o caso em breve, quando falarmos de lançamento oblícuo.
Se $\vec{v}$ é um vetor cujo "tamanho" (módulo) igual à $|\vec{v}|$. O que obteremos se multiplicarmos o escalar $\frac{1}{|\vec{v}|}$ pelo vetor $\vec{v}$? Vamos verificar:
Ao multimplicarmos um vetor por um escalar, sua direção não muda; como o escalar é maior que zero, uma vez que $|\vec{v}| > 0$ se $\vec{v} \neq \vec{0}$, seu sentido também não muda; por fim vamos calcular o módulo deste novo vetor:
$$\left | \frac{1}{|\vec{v}|} \cdot \vec{v} \right | = \frac{1}{|\vec{v}|} \cdot |\vec{v}| = 1$$
Resumindo: o vetor unitário de um vetor $\vec{v}$ não nulo possui as seguintes propriedades:
possui a mesma direção e sentido do vetor $\vec{v}$
possui módulo unitário, isto é, seu "comprimento" tem tamanho igual à uma unidade
Um vetor pode ter qualquer dimensão, isto é, estamos analisando o caso de pontos no espaço tridimensional, porém podemos entender como "espaço" não somente os formados por unidades de distâncias, como o metro. Podemos, por exemplo, pensar em um espaço cujas dimensões são unidades de força (por exemplo, o newton), assim o vetor unitário terá dimensão igual à 1 newton.
SISTEMA CARTESIANO DE COORDENADAS
Vamos agora quase entrar na geometria analítica! Comecemos pelo plano cartesiano em duas dimensões.
Seja um ponto A. Como podemos localizá-lo no espaço? Primeiro temos que dar uma referência, dizer onde este ponto se localiza em relação à alguma coisa. Vamos começar criando um sistema de endereço para este ponto: tracemos duas retas perpendiculares entre si conforme a figura abaixo.
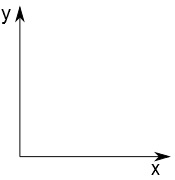
Ao eixo horizontal, ao qual atribuímos uma reta real e ao valor numérico desta reta real chamaremos de x, daremos o nome de eixo das abscissas. Ao eixo vertical daremos o nome de eixo y ou eixo das ordenadas.
Suponha que este ponto A esteja representado na figura. Trace uma reta paralela ao eixo y e que passe pelo ponto A; o ponto de interseção entre esta reta e o eixo x nós damos o nome de coordenada x do ponto A. Analogamente, trace uma reta paralela ao eixo dos x que passe pelo ponto A; o ponto de interseção entre esta reta e o eixo y é chamada de coordenada y do ponto. Podemos resumir esta informação dizendo que o ponto A possui coordenadas (x;y). Veja a figura a seguir.
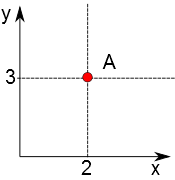
No desenho acima podemos dizer que a abscissa do ponto A é igual à 2 e a ordenada é igual à 3 ou, em notação mais compacta, o ponto A possui coordenadas (2;3). Usaremos aqui o ";" para separar x e y, embora há autores, principalmente extrangeiros, que usam ",". Esta opção foi feita para não confundir com o separador usual em português para representar casas decimais. Em inglês, 1,5 (um e meio) é representado como 1.5 (observe a maioria das calculadoras).
À esse ponto podemos sempre associar um segmento orientado que parte sempre do ponto (0;0) e termina em A. Este segmento é equipolente a uma infinidade de outros seguimentos e portanto pode ser usado como representante de um vetor (conjunto). Também é fácil perceber que para todo seguimento orientado de comprimento não nulo, é sempre possível encontrar um seguimento orientado equipolente que parte da origem do sistema de coordenadas e termina em um ponto genérico A (aqui, não nos referimos ao ponto (2;3)). Resumindo: podemos "colocar" todo e qualquer vetor com origem coincidente ao ponto (0;0), inclusive o vetor nulo $\vec{0}$.
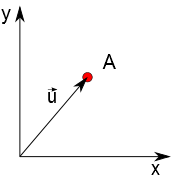
Vamos supor que exista um vetor $\vec{x}$ que está representado por um seguimento orientado contido no eixo x. Podemos então escrever um vetor unitário, ao qual daremos o nome de vetor $\hat{i}$ que será definido, conforme visto quando falado de vetor unitário, da seguinte forma:
$$|\hat{i}| = \left | \frac{1}{|\vec{x}|} \cdot \vec{x} \right | = \frac{1}{|\vec{x}|} \cdot |\vec{x}| = 1$$
Identicamente, podemos falar em vetor unitário $\hat{j}$ do vetor $\vec{y}$:
$$|\hat{j}| = \left | \frac{1}{|\vec{y}|} \cdot \vec{y} \right | = \frac{1}{|\vec{y}|} \cdot |\vec{y}| = 1$$
Posso então dizer que o vetor $\vec{u}$ pode ser obtido somando-se dois vetores perpendiculares entre si sendo um paralelo ao $\vec{x}$ e outro paralelo ao eixo $\vec{y}$.
Na figura a seguir está representado três vetores $\hat{j}$, cujo módulo é unitário, e por isso pode ser colocado entre duas unidades do eixo das ordenadas. No eixo horizontal está representado dois vetores $\hat{i}$.
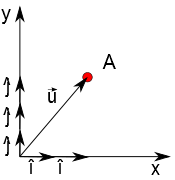
Observe a seguir uma segunda representação possível para um vetor:
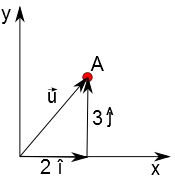
Assim podemos dizer que o vetor $\vec{u}$ é a soma de dois outros vetores: $2\hat{i}$ e $3\hat{j}$. Ou seja:
$$\vec{u} = 2\hat{i} + 3\hat{j}$$
Provavelmente você já deve ter tido contato com esta notação. Então daremos mais uma, um pouco mais compacta.
Seja um vetor $\vec{u} = x\hat{i} + y\hat{j}$, ele pode ser representados a seguinte forma:
$$\vec{u} = x\hat{i} + y\hat{j} = \left \{ x;y\right \}$$
Aqui usamos as chaves "{" e "}" para não confundir com a representação de ponto (x;y).
Bom, mas sistema coordenado em duas dimensõe não tem graça... Nós vivemos em um mundo de três dimensões espaciais, não é? Então vamos estudar o sistema em três dimensões.
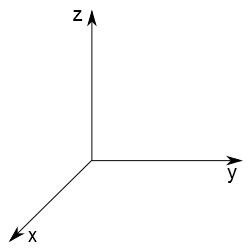
Para isso acrescentemos mais um eixo no nosso sistema de coordenadas. Este novo eixo será o eixo z ou eixo das cotas e localizamos a sua direção fazendo uso da regra da mão direita. Para determinar a direção do eixo z, primeiro escolha as direções dos eixos x e y. Por exemplo, seja o seguinte conjunto de eixos coordenados:

Para isso, abra sua mão deixando todos os seus dedos juntos, com excessão do dedão que deverá apontar numa direção perpendicular aos demais dedos. Aponte com seus dedos na direção do eixo x e gire em direção ao eixo y percorrendo o menor ângulo. A direção de seu dedão irá apontar o eixo z. Observe que na figura acima, o eixo z estará perpendicular ao plano que contem os eixos x e y!
Pratique a regra da mão direita! Ela lhe será extremamente importante!!!
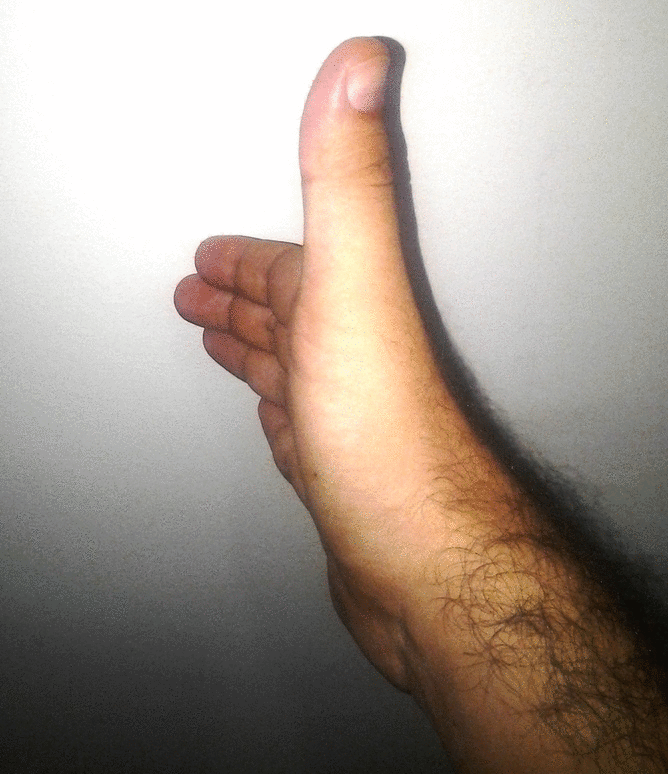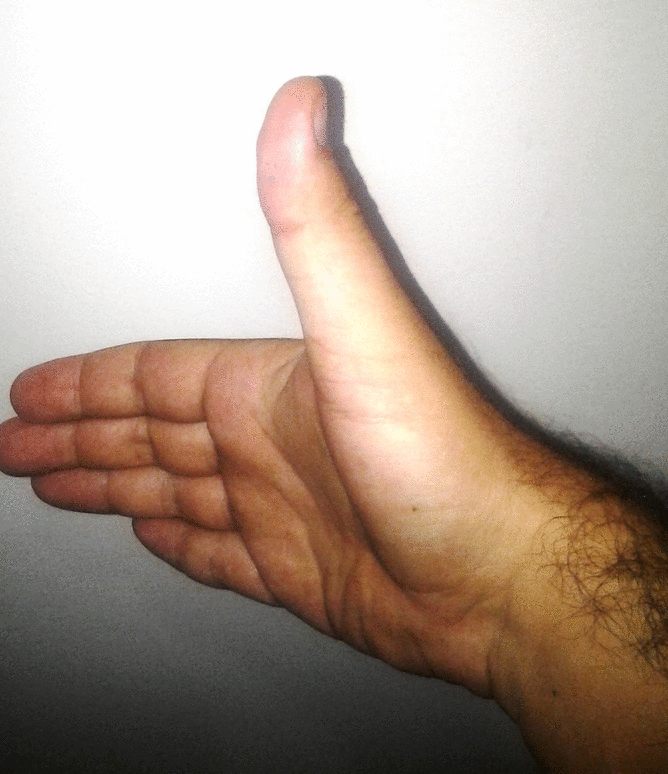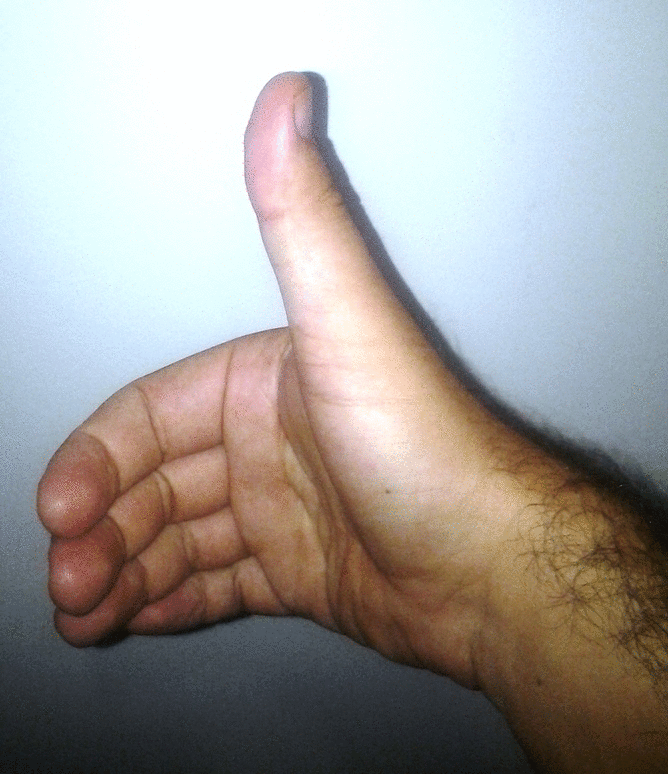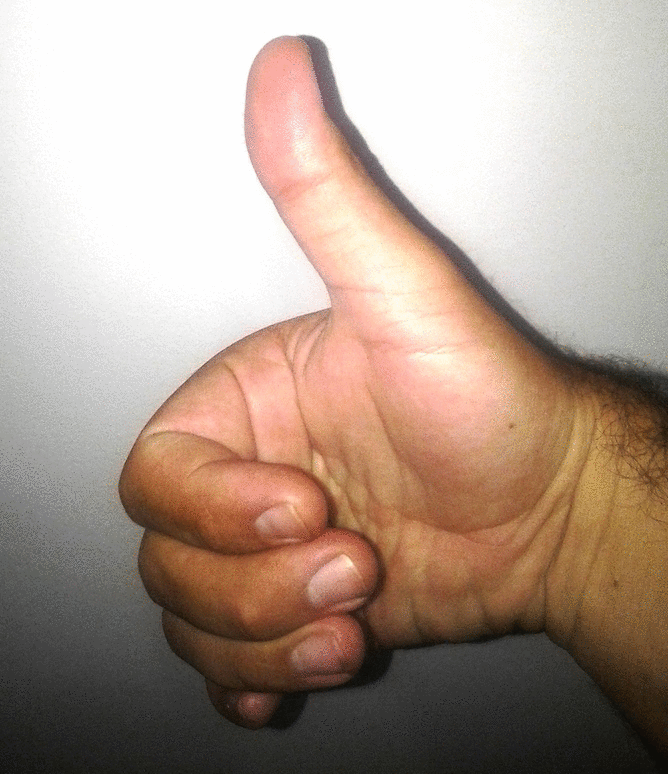
Tradicionalmente usa-se o eixo z na vertical, assim o esquema abaixo é uma alternativa para representar o sistema de eixos coordenados em três dimensões:
Extendendo o conceito de vetores unitarios ligados aos eixos coordenados (estes vetores também são chamados versores), na direção do eixo das cotas temos o vetor unitário $\hat{k}$. Assim podemos escrever qualquer vetor em três dimensões como se segue:
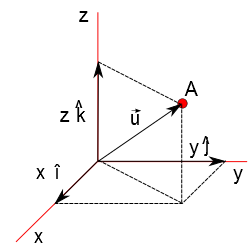
$$\vec{u} = x\hat{i}+y\hat{j}+z\hat{k} = \left \{ x;y;z \right \}$$
Na figura anterior foram omitidas as setas que orientam os eixos x, y e z apenas para evitar confusões futuras. Aproveite também para treinar a "regra da mão direita".
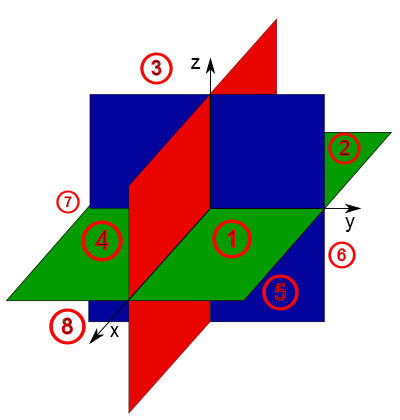
Vamos agora falar dos octantes: a figura abaixo mostra parte dos três planos (que são infinitos) formados pelos três eixos coordenados. Estes três planos dividem o espaço em oito partes tais que para sair de qualquer uma delas e chegar à outra, você deve atravessar algum plano. Nela estão apresentados os "números" para cada octante, isto é, 1 parta o 1$^o$, 2 para o 2$^o$ e assim por diânte. É importante saber a nomenclatura de cada octante para o caso em que os dados que você tem em mãos descrevem seus dados usando estes nomes, mas na física esta nomenclatura será rara, mas mesmo assim vale apena saber, mesmo que somete para problemas específicos (que pode aparecer em questões de matemática).
Introduzida a ideia de plano de coordenada cartesiano, vamos utilizá-lo para descrever algumas figuras mais simples da geometria. Dentre elas, vamos aprender a encontrar a equação de uma reta e de um plano usando vetores. Vamos começar lembrando da equação de distância de ponto à ponto e depois, de forma bem imediata, encontraremos a equação da circunferência e da esfera.
Cabe aqui acrescentar mais um novo assunto: os cossenos diretores.
Observe a figura abaixo. Nela temos um vetor $\vec{v}$ representado em um sistema de eixos cartesianos bem como os ângulos entre cada um dos eixos:
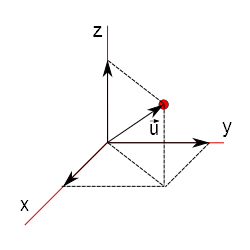
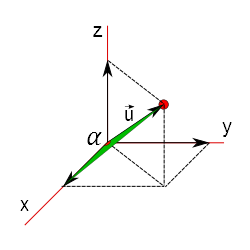
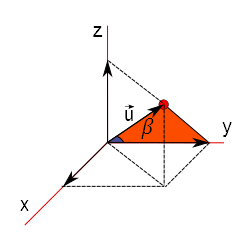
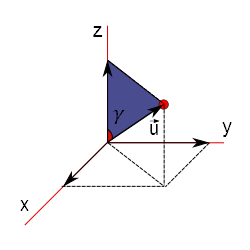
Digamos que você tenha o vetor $\vec{u}$:
$$\vec{u}=x\hat{i}+y\hat{j}+z\hat{k}$$
Pode-se calcular os cossenos diretores da seguinte maneira:
$$\rm{cos}\alpha = \frac{x}{|\vec{u}|}$$
$$\rm{cos}\beta = \frac{y}{|\vec{u}|}$$
$$\rm{cos}\gamma = \frac{z}{|\vec{u}|}$$
Estes são chamados cossenos diretores e voltaremos a faler deles futuramente.
DISTÂNCIA PONTO À PONTO
São dados dois pontos no espaço, sejam eles os pontos A e B. Se A possui coordenadas ($x_A;y_A;z_A$) e B possui coordenadas ($x_B;y_B;z_B$), qual é a distândia entre os dois pontos?
Para simplificar, vamos primeiramente determinar a distância de um ponto P com coordenadas ($x;y;z$) até a origem do sistema de coordenadas escolhido.
Observe o esquema abaixo.
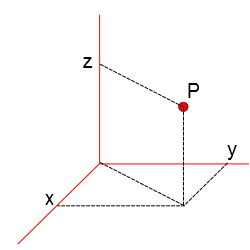
Pelo Teorema de pitágoras, podemos determinar a distância entre a projeção do ponto P sobre oplano xy e a origem do sistema de coordenadas:
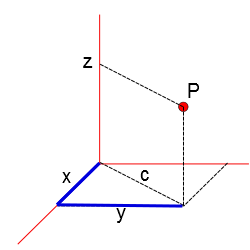
$$c^2=x^2+y^2$$
Entretanto, a distância que queremos encontrar, $d$, pode ser determinada pelo triângulo da figura a seguir:
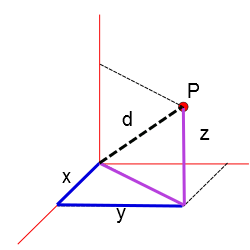
$$d^2=z^2+c^2$$
Mas sabemos que $c^2=x^2+y^2$, tentão: $$d^2=x^2+y^2+z^2$$
Seguindo este mesmo raciocínio, podemos encontrar a distância entre os pontos A e B. Observe que a equação acima é uma extensão do Teorema de Pitágoras.
Podemos reescrever a equação acima substituindo $x$ por $\Delta x$, $y$ por $\Delta Y$ e $Z$ por $\Delta Z$ para quaisquer dois pontos. Assim pode-se obter que a distância entre os pontos A e B é dada por:
$$d_{AB}=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
E assim temos a equação que nos diz a distância entre dois pontos.
EQUAÇÃO DA CIRCUNFERÊNCIA E DA ESFERA
Observe a figura abaixo
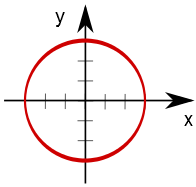
Nela temos representado uma circunferência de raio $R$. O que ela tem em comum com o tópico passado: "distância ponto à ponto"?
A resposta é que a circunferência pode ser descrita como sendo o lugar geométrico equidistânte de um ponto, isto é, todos os pontos da figura anterior possuem a mesma distância do cento do nosso sistema de coordenadas.
Assim podemos utilizar o Teorema de Pitágoras para descobrir quais os pontos pertence à circunferência. Vejamos:
$$R^2=x^2+y^2$$
Na verdade acabou! É só isso, com a diferênça de que agora $x$ e $y$ são variáveis (ou coordenadas de qualquer ponto contido na circunferência) e não coordenadas de um ponto fixo.
Se pensarmos em uma circunferência com centro não coincidente à origem de nosso sistema de coordenadas, podemos substiruir $x$ por $\Delta x$ e $y$ por $\Delta Y$, para que componham os catetos do triânculo retângulo:
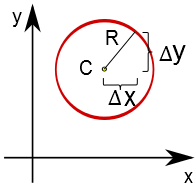
Sendo C = ($x_C;y_C$) o centro da circunferência, então:
$$R^2=(\Delta x)^2 + (\Delta y)^2$$
$$R^2=(x-x_C)^2 + (y-y_C)^2$$
Esta é a equação da circunferência.
A equação da esfera é análiga:
Seja uma superfície cujos pontos que a constituem sejam todos equidistantes de um ponto C = ($x_C;y_C$;z_C). Este ponto C é o centro da superfície e a superfície é uma esfera. Seja $R$ o raio desta esfrerae, portanto, a distância de todos os pontos da superfície ao centro C.
Basta aplicar o Teorema de Pitágoras em três dimensões:
$$R^2=(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2$$
$$R^2=(x-x_C)^2 + (y-y_C)^2 + (z-z_C)^2$$
Para resumir, temos então que:
$$R^2=(x-x_C)^2 + (y-y_C)^2 \text{ é a equação da circunferência}$$
$$R^2=(x-x_C)^2 + (y-y_C)^2 + (z-z_C)^2 \text{ é a equação da esfera}$$
EQUAÇÃO VETORIAL DA RETA
Vamos agora à uma aplicação do uso de vetores: vamos encontrar uma equação vetorial para representarmos uma reta. Mas antes disso, temos que definir o que seria uma soma de um ponto com um vetor. Esta definição entretanto é simples.
Seja um vetor $\vec{v}$ que pode ser representado pelo segmento orientado $\vec{AB}$. Podemos dizer que
$$B=A+\vec{v}$$
isto é, estamos somando ao ponto A um vetor $\vec{v}$ e obtendo um segundo ponto B. Pode-se verificar geometricamente que o ponto A é único.
Esta operação possui algumas propriedades, semelhante às dos vetores. São elas:
- $B+\vec{0}=B$
- $B + \vec{u}=B + \vec{v} \Rightarrow \vec{u}=\vec{v}$
- $(P+\vec{u})+\vec{v}=P+(\vec{u}+\vec{v})$
- $A+ \vec{v} =B+\vec{v} \Rightarrow A=B$
- $(P-\vec{v})+\vec{v}=P$
Assim, seja um ponto A ao qual somamos um vetor $\vec{v}$. Encontraremos apenas um ponto B, mas se multiplicarmos o vetor $\vec{v}$ por um escalar $\alpha$ qualquer, encontraremos outro ponto. Chamemos este ponto, resultado da soma, de ponto X. Assim temos:
$$X=A+\alpha \cdot \vec{v} $$
Se alterarmos o valor de $\alpha$ livremente, ou seja, se $\alpha$ puder assumir qualquer valor dos números reais, o ponto X irá variar ao longo de uma reta que passa pelo ponto A e é paralela ao vetor $\vec{v}$, ou seja, a equação acima é a equação da reta que contém o ponto A e é paralela ao vetor $\vec{v}$. Observe a figura abaixo na qual há uma animação para representar esta ideia:
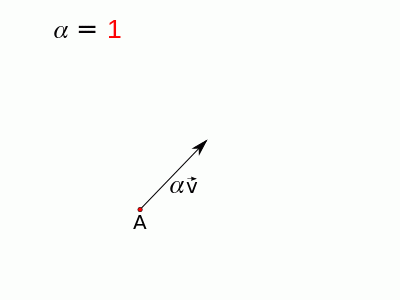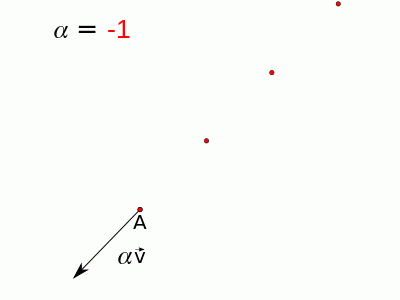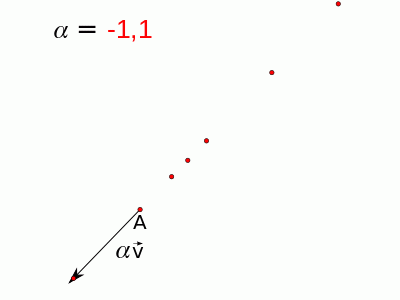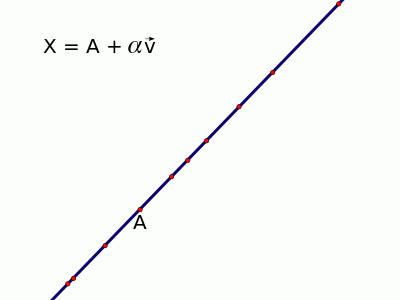
Assim, esta é a equação vetorial da reta:
$$\boxed{X=A+\alpha \cdot \vec{v}}$$
Exemplo
Encontre a equação da reta que passa pelo ponto $A=(1;0;1)$ e $B=(0;1;0)$.
RESOLUÇÃO:
Observe que o vetor $$\vec{AB}={B_x-A_x;B_y-A_y;B_z-A_z}={⁻1;1;-1}$$ é um vetor paralelo à reta, pois o ponto B é a soma $A+\vec{AB}$. Assim a equação da reta será:
$$X=A+\alpha \cdot \vec{v} \Rightarrow$$
$$X=(1;0;1)+\alpha \cdot \left \{-1;1;-1 \right \} \Leftrightarrow$$
$$X=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \}$$
Note que o ponto X é um ponto pertencente à reta e podemos escrevê-lo como sendo $X=(x;y;z)$ em que x, y e z são as coordenadas do ponto X. Assim, podemos reescrever a equação acima e transformá-la em um sistema de equações:
$$X=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \} \Leftrightarrow$$
$$(x;y;z)=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \}\Leftrightarrow$$
$$
\left\{\begin{matrix}
x & = & 1 & + & \alpha \cdot& \! \! \! \! (-1)\\
y & = & 0 & + & \alpha \cdot & 1\\
z & = & 1 & + & \alpha \cdot & \! \! \! \! (-1)
\end{matrix}\right.
\Leftrightarrow
$$
$$
\boxed{
\left\{\begin{matrix}
x & = & 1 & - & \alpha\\
y & = & & & \alpha\\
z & = & 1 & - & \alpha
\end{matrix}\right.
}
$$
Esta é a equação da reta em três dimensões! Como temos um parâmetro (o escalar $\alpha$), esta equação recebe o nome de equação paramétrica.
EQUAÇÃO VETORIAL DO PLANO
Usando a mesma ideia que a anterior, podemos representar a equação de um plano da seguinte forma:
$$\boxed{X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u}}$$
Note que a soma dos vetores $\alpha \cdot \vec{v} +\beta \cdot \vec{u}$, em que $\beta$, assim como $\alpha$, é um escalar, nos fornecerá um ponto X pertencente a um plano que é simultaneamente paralelo à $\vec{u}$ e $\vec{v}$ e que contém o ponto A. Assim, variando livremente os escalares $\alpha$ e $\beta$, encontraremos todos os pontos que define um único plano.
Exemplo 1
Determine a equação paramétrica do plano que passa pelos pontos $A=(7;7;1)$ e é paralelo aos vetores $\vec{v}= \left \{1;1;1 \right \} $ e $\vec{u}= \left \{-1;0;1 \right \} $.
RESOLUÇÃO:
Substituindo os dados na equação vetorial do plano teremos:
$$X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u} \Leftrightarrow$$
$$(x;y;z)=(7;7;1)+\alpha \cdot \left \{1;1;1 \right \} +\beta \cdot \left \{-1;0;1 \right \} \Leftrightarrow$$
$$(x;y;z)=(7;7;1)+ \left \{\alpha;\alpha;\alpha \right \} + \left \{-\beta;0;\beta \right \} \Leftrightarrow$$
$$
\boxed{
\left\{\begin{matrix}
x & = & 7 & + & \alpha & - & \beta \\
y & = & 7 & + & \alpha & \\
z & = & 1 & + & \alpha & + & \beta
\end{matrix}\right.
}$$
Exemplo 2
Encontre a equação do plano que passa pelo ponto $A=(1;0;1)$ e $B=(0;1;-1)$ e é paralelo ao segmento CD onde $C=(1;2;1)$ e $D=(0;1;0)$.
RESOLUÇÃO:
Primeiro, encontremos dois vetores paralelos ao plano para que possamos usar a equação vetorial do plano:
$$\vec{AB}= \left \{-1;1;0 \right \} = \vec{u}$$
$$\vec{CD}= \left \{1;1;1 \right \} = \vec{v}$$
Agora que temos os dois vetores, basta escolher um ponto pertencente ao plano (pode ser A ou B). Escolhendo o ponto A:
$$X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u} \Leftrightarrow$$
$$(x;y;z)=(1;0;1)+\alpha \cdot \left \{-1;1;0 \right \} +\beta \cdot \left \{1;1;1 \right \} \Leftrightarrow$$
$$(x;y;z)=(1;0;1)+ \left \{-\alpha;\alpha;0 \right \} + \left \{\beta;\beta;\beta \right \} \Leftrightarrow$$
$$
\boxed{
\left\{\begin{matrix}
x & = & 1 & - & \alpha & + & \beta \\
y & = & & & \alpha & + & \beta \\
z & = & 1 & & & + & \beta
\end{matrix}\right.
}$$
Exercício
Encontra a equação do plano que contém os ponto A, B e C para cada item a seguir:
a) $A=(1;0;1)$, $B=(2;1;-1)$ e $C=(1;-1;0)$
b) $A=(-1;2;-5)$, $B=(-1;1;3)$ e $C=(3;-1;1)$
c) $A=(-4;4;-12)$, $B=(2;-2;6)$ e $C=(1;-1;3)$. Você chegou em algum resultado estranho? Determine a equação da reta que passa pelos pontos A e B e verifique se é a mesma equação da reta que contém os pontos A e C.
SISTEMA CILÍNDRICO DE COORDENADAS
Vamos agora comentar brevemente sobre outros sintemas de coordenadas.
Até agora nós vimos apenas um, que servirá de base para construir qualquer outra noção de sistema de referencial, inclusive o sistema de coordenadas cilíndrico (ou sistema cilíndrico de coordenadas).
A ideia é tentar localizar um ponto no espaço de coordenadas cartesianas ($x;y;x$) e determinar a posição deste mesmo ponto usando outro sistema. Vamos começar então.
Observe a figura abaixo. Nela está representado um cilindro de raio $s$ e o ângulo $\varphi$. A altura coincide com a cota z do sistema cartesiano e $\varphi$ chama-se ângulo azimutal.
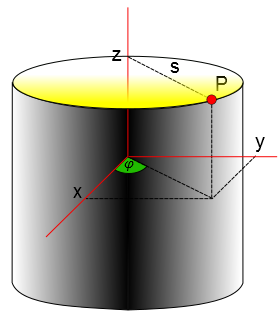
Cada pondo de coordenadas ($x;y;z$) pode ser associado à um ponto de coordenadas ($s;\varphi;z$). O raio $s$ pode variar de zero à $+\infty$, $0 \leqslant \varphi \leqslant 2\pi$ enquanto que $z$ pode ir de $-\infty$ à $+\infty$, como no caso de $z$ no sistema cartesiano. Observe a figura e veja que as relações abaixo são verdadeiras:
$$\left\{\begin{matrix}
x=s&\rm{cos}\varphi\\
y=s&\rm{sen}\varphi\\
z=z&
\end{matrix}\right.$$
Estas relações são na verdade uma maneira de mudar de referencial. Tente isolar o raio $s$ e o ângulo $\varphi$. Se conseguir, terá um conjunto de três equações que mudam do sistema cilíndrico de coordenadas para o sistema cartesiano.
SISTEMA ESFÉRICO DE COORDENADAS
Semelhante ao sistema cilíndrico, o sistema esférico tem como base uma esfera com centro no ponto (0;0;0) e raio $r$. O raio vetor $\vec{r}$ que localiza um ponto qualquer na esfera forma um ângulo $\theta$ com o eixo vertical e a projeção do raio vetor no plano xy forma um ângulo $\varphi$ com o eixo x.
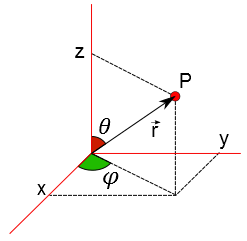
Este é o sistema de referência que se utiliza para localizar um corpo na superfície do planeta Terra se você adotar como eixo z o eixo de rotação da Terra e o polo norte na parte de z positivo. Talvez por esta razão, o ângulo $\theta$ chama-se ângulo polar. O ângulo formado entre a projeção de $\vec{r}$ e o eixo x, $\varphi$, chama-se ângulo azimutal assim como em coordenadas cilíndricas.
A diferença entre as coordenadas geográficas esféricas e as coordenadas esféricas é que nestas últimas, $r$ varia de zero á $\infty$, $0\leq \theta \leq \pi$ e $0\leq \varphi \leq 2\pi$. Já nas coordenadas geográficas, $r$ é o raio da Terra (aproximadamente constante); o ângulo polar é substituído por outro (latitudinal) que é medido a partir da linha do equador indo de zero (na linha do equador) até $+\pi/2$ no polo norte e de zero à $-\pi/2$ no polo sul; por fim o ângulo equivalente ao azimutal é o longitudinal que tem como zero o meridiano que passa na Inglaterra na cidade de Greenwich e varia de zero a $+\pi$ na direção leste e de zero a $-\pi$ na direção oeste.
Verifique as equações a seguir de transformação de sistema de coordenadas:
$$ \left\{\begin{matrix}
x=r&\rm{sen}\theta&\rm{cos}\varphi\\
y=r&\rm{sen}\theta&\rm{sen}\varphi\\
z=r&\rm{cos}\theta
\end{matrix}\right.$$
CENTRO DE MASSA
Centro de massa está intimamente ligado ao conceito de centro de gravidade e, por hora, consideraremos ambos como sendo sinônimos (eles são diferentes e ficará mais claro o conceito de centro de massa quando estudar gravitação universal; já centro de gravidade é mais intuitivo). Vamos então tentar entender, de forma mais ou menos intuitiva, o que é centro de gravidade.
Imagine que você queira pendurar uma vassoura de piaçava utilizando um barbante. Onde você deve prender o barbante? Certamente mais próximo às fibras de piaçava que da ponta do cabo e a resposta mais intuitiva é que "a região com as fibras são mais 'pesadas' que o cabo". Vamos dizer diferente: divida a vassoura no meio deixando puco mais da metade do cabo de um lado e o restante do outro. Na verdade a parte com as fibras de piaçava possuem mais massa! Assim você deve amarra a vassoura em algum ponto mais próximo das fibras.
Considere um ponto A de coordenadas ($x_A;y_A;z_A$) e B de coordenadas ($x_B;y_B;z_B$). Coloquemos um corpo muito pequeno (que chamaremos de corpo pontual) de massa $m_A$ em A e um corpo pontual de massa $m_B$ em B. O centro de massa (ou, mais intuitivamente, caso ambos os corpos estivessem presos por uma haste muito leva, o ponto onde deveríamos prender a haste para permanecer em equilíbrio) é dado por:
$$CM_1=\frac{m_AA+m_BB}{m_A+m_B}$$
Entenda que estamos trabalhando com pontos.
Se colocarmos uma terceira massa $m_C$ em um ponto $C=(x_C;y_C;z_C)$, teríamos:
$$CM_2=\frac{(m_A+m_B)CM_1+m_CC}{(m_A+m_B)+m_C}\Rightarrow $$
$$CM_2=\frac{(m_A+m_B)\frac{m_AA+m_BB}{m_A+m_B}+m_CC}{m_A+m_B+m_C}\Rightarrow $$
$$CM_2=\frac{m_AA+m_BB+m_CC}{m_A+m_B+m_C}$$
Assim, se escolhermos $n$ pontos, $P_1$ e nele colocarmos uma massa $m_1$, $P_2$ e nele colocarmos uma massa $m_2$, $P_3$ e nele colocarmos uma massa $m_3$, e assim até o n-ésimo ponto $P_n$ com massa $m_n$ teríamos como centro de massa $CM$ o ponto assim calculado:
$$ CM=\frac{\sum_{i=1}^{n} m_iP_i}{ \sum_{i=1}^{n} m_i}$$
É importante observar que acima temos uma notação compacta e que o ponto $CM$ na verdade é o ponto ($x_{CM};y_{CM};z_{CM}$) e a equação para as coordenadas ficaria como se segue:
$$ \left\{\begin{matrix}
x_{CM}=\frac{\sum_{i=1}^{n} m_ix_i}{ \sum_{i=1}^{n} m_i}\\
y_{CM}=\frac{\sum_{i=1}^{n} m_iy_i}{ \sum_{i=1}^{n} m_i}\\
z_{CM}=\frac{\sum_{i=1}^{n} m_iz_i}{ \sum_{i=1}^{n} m_i}
\end{matrix}\right.$$
Como um exemplo, vamos mostrar que se tivermos três pontos A, B e C não alinhados em cada um um objeto pontual de massa $m$. Se traçarmos uma linha de um dos pontos (por exemplo, o ponto A) passando pelo centro de massa dos outros dois (isto é, pelo ponto médio), o centro de gravidade se encontrará a uma distância $x$ do ponto médio de B e C e $2x$ do ponto A.
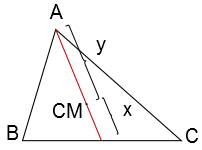
Na verdade a solução é bem simples. Primeiramente, você não precisa se ater aos sistemas de coordenas, pois o que as equações acima nos mostra é que as massas atuam como uma média ponderada. Então, pense em um eixo coincidente com a reta que traçamos (chamada de bissetriz) e chame de $y$ a distância do centro de massa $CM$ até o ponto A e de $x$ a distância entre $CM$ e o ponto médio do segmento BC. Adote como sendo 0 (zero) o valor da coordenada do $CM$. Então:
$$CM=\frac{2mx+my}{2m+1m}\Rightarrow $$
$$0=\frac{2x+y}{3}\Rightarrow $$
$$0=2x+y\Rightarrow $$
$$y=-2x$$
Observe que o sinal negativo se deve por termos escolhido como origem o ponto $CM$, assim se $Y$ for positivo, $x$ é negativo, e vice-versa.
DEMONSTRAÇÃO DA LEI DOS COSSENOS
Vamos à uma breve demonstração da lei dos cossenos. Para isso, seja um vetor $\vec{u}$ e um vetor $\vec{v}$ quaisquer, representados na figura a seguir.
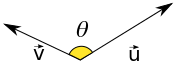
Podemos escolher um referencial qualquer para representarmos estes dois vetores em termos de suas coordenadas. Escolheremos então um referencial no qual o vetor $\vec{u}$ esteja contido no eixo x. Assim, em termos de suas coordenadas e baseado na figura abaixo, teremos:
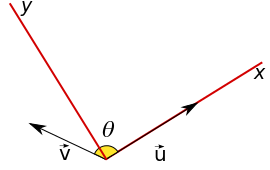 $$\left \{
\begin{matrix}
\vec{u} & = & u\cdot \hat{i}&\\
\vec{v} & = & v\cdot \rm{cos}\theta\cdot\hat{i} &+ &v \cdot \rm{sen}\theta\cdot\hat{j}
\end{matrix}\right.$$
$$\left \{
\begin{matrix}
\vec{u} & = & u\cdot \hat{i}&\\
\vec{v} & = & v\cdot \rm{cos}\theta\cdot\hat{i} &+ &v \cdot \rm{sen}\theta\cdot\hat{j}
\end{matrix}\right.$$
A soma $\vec{S}$ desses vetores será dada por:
$$
\vec{S}=\vec{u}+\vec{v}=(u+v\cdot cos\theta) \cdot\hat{i} + v \cdot sen \theta\cdot\hat{j}
$$
O módulo ao quadrado da soma ($|\vec{S}|^2$ ou $S^2$) pode ser determinado:
$$
|\vec{S}|^2=(u+v\cdot cos \theta)^2 + ( v \cdot sen\theta)^2 \Leftrightarrow
$$
$$
S^2=u^2+2uv\cdot cos\theta+ v^2\cdot cos^2\theta + v^2 \cdot sen^2\theta \Leftrightarrow
$$
$$
S^2=u^2+2uv\cdot cos\theta+ v ^2(cos^2\theta +sen^2 \theta)\Leftrightarrow
$$
$$
\boxed{S^2=u^2+ v ^2+2uv\cdot cos\theta}
\; \; \; \; \; \; \;
\boxed{}
$$
DEMONSTRAÇÃO DA LEI DOS SENOS
A lei dos senos pode ser demonstrada rapidamente utilizando-se um triângulo qualquer. Como queremos uma aplicação vetorial, comecemos com o triângulo a seguir cujos lados estão representados os vetores $\vec{u}$, $\vec{v}$ e $\vec{w}$, cujos módulos são, respectivamente, $u$, $v$ e $w$ e representam os lados do triângulo, que chamaremos simplesmente de lados $u$, $v$ e $w$.

Observe que a altura do triângulo em relação ao lado $w$ é:
$$
u\cdot sen\beta=v \cdot sen\alpha
$$
A altura em relação à $v$ será:
$$
u\cdot sen\delta=w \cdot sen\alpha
$$
Por fim, a altura em relação à $u$ será:
$$
w\cdot sen\beta=v \cdot sen\delta
$$
Essas três equações podem ser reescrita conforme se segue:
$$
\left\{\begin{matrix}
\frac{u}{sen\alpha} & = & \frac{v}{sen\beta}\\
\frac{u}{sen\alpha} & = &\frac{w}{sen\delta} \\
\frac{w}{sen\delta}& = &\frac{v}{sen\beta}
\end{matrix}\right.
$$
A partir deste sistema, a lei dos senos é imediata
$$
\frac{u}{sen\alpha} = \frac{v}{sen\beta}= \frac{w}{sen\delta}
\; \; \; \; \; \boxed{}
$$
BIBLIOGRAFIA
- Paulo Boulos, Ivan de Camargo, GEOMETRIA ANALÍTICA UM TRATAMENTO VETORIAL, 3$^a$ ed., pp. 1 - 17.
Talvez você se lembre da lei dos senos na matemática.
Observer a figura abaixo. Nela temos um triângulo com os respectivos ângulos internos.

A lei dos senos nos da a seguinte relação entre os ângulos internos de um triângulo e seus lados: $$\frac{\rm{a}}{\rm{sen}{\alpha}} = \frac{b}{\rm{sen}{\beta}} = \frac{d}{\rm{sen}{\delta}}$$
Vamos substituir os lados seste triângulo por vetores. Ao fazer isso pode-se verificar que a soma dos três vetores será nula: $$\vec{u} + \vec{v} + \vec{w} = \vec{0}$$

E a lei dos senos na matemática se mantém, bastando substituir os lados dos triângulos pelos módulos dos vetores que os compõem. Ou seja:$$\frac{|\vec{u}|}{\rm{sen}{\alpha}} = \frac{|\vec{v}|}{\rm{sen}{\beta}} = \frac{|\vec{w}|}{\rm{sen}{\delta}}$$
Mas se colocarmos os vetores todos com uma origem em comum, obtemos novamente a equação acima. Para verificar isso, observe o desenho a seguir.

Lembrando que $\rm{sen}(180^o - \alpha) = \rm{sen{\alpha}}$, podemos manter todos os denominadores na lei dos senos e substituir os numeradores pelos respectivos módulos dos lados dos triângulos: $$\frac{|\vec{u}|}{\rm{sen}{\alpha}} = \frac{|\vec{v}|}{\rm{sen}{\beta}} = \frac{|\vec{w}|}{\rm{sen}{\delta}}$$
MULTIPLICAÇÃO POR ESCALAR
Vamos agora ver as propriedades de multiplicação de um vetor por um escalar.
A multiplicação de um vetor por um escalar (um número real, i.e., pode ser negativo, nulo, inteiro, irracional como o $\pi$, etc) tem como propriedade alterar apenas o módulo e o sentido de um vetor, sendo incapaz de mudar sua direção.
Temos então as seguintes propriedades:
Seja $\alpha \in \Re$ e um vetor $\vec{v} \in V^3$ (isto é, ao espaço formado por todos os vetores tridimensionais), então $\alpha \vec{v}$ é a expressão que representa a multiplicação do vetor $\vec{v}$ pelo escalar $\alpha$.
a) $\alpha \vec{v}$ é paralelo à $\vec{v}$
b)$\alpha \vec{v}$ e $\vec{v}$ possuem mesmo sentido se $\alpha > 0$ e possuem sentido oposto se $\alpha < 0$
c)$|\alpha \vec{v}| = |\alpha| \cdot |\vec{v}|$
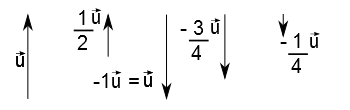
- Propriedade Distributiva 1
- Propriedade Distributiva 2
- Propriedade da existência do Elemento Neutro
- Propriedade Associativa
$$\alpha (\vec{u} + \vec{v}) = \alpha \vec{u} + \alpha \vec{v} $$

A figura acima representa esta propriedade para o caso em que $\alpha > 0$ e a figura abaixo para o caso em que $\alpha < 0$

$$(\alpha + \beta) \vec{u} = \alpha \vec{u} + \beta \vec{u}$$

$$1 \cdot \vec{v} = \vec{v}$$
$$(\alpha \beta) \vec{v} = \alpha (\beta \vec{v}) = \beta (\alpha \vec{v})$$
VETOR UNITÁRIO
Vamos agora introduzir o conceito de vetor unitário, uma vez que será útil sempre que fizermos a decomposição de vetores, como será o caso em breve, quando falarmos de lançamento oblícuo.
Se $\vec{v}$ é um vetor cujo "tamanho" (módulo) igual à $|\vec{v}|$. O que obteremos se multiplicarmos o escalar $\frac{1}{|\vec{v}|}$ pelo vetor $\vec{v}$? Vamos verificar:
Ao multimplicarmos um vetor por um escalar, sua direção não muda; como o escalar é maior que zero, uma vez que $|\vec{v}| > 0$ se $\vec{v} \neq \vec{0}$, seu sentido também não muda; por fim vamos calcular o módulo deste novo vetor: $$\left | \frac{1}{|\vec{v}|} \cdot \vec{v} \right | = \frac{1}{|\vec{v}|} \cdot |\vec{v}| = 1$$
Resumindo: o vetor unitário de um vetor $\vec{v}$ não nulo possui as seguintes propriedades:
Um vetor pode ter qualquer dimensão, isto é, estamos analisando o caso de pontos no espaço tridimensional, porém podemos entender como "espaço" não somente os formados por unidades de distâncias, como o metro. Podemos, por exemplo, pensar em um espaço cujas dimensões são unidades de força (por exemplo, o newton), assim o vetor unitário terá dimensão igual à 1 newton.
SISTEMA CARTESIANO DE COORDENADAS
Vamos agora quase entrar na geometria analítica! Comecemos pelo plano cartesiano em duas dimensões.
Seja um ponto A. Como podemos localizá-lo no espaço? Primeiro temos que dar uma referência, dizer onde este ponto se localiza em relação à alguma coisa. Vamos começar criando um sistema de endereço para este ponto: tracemos duas retas perpendiculares entre si conforme a figura abaixo.

Ao eixo horizontal, ao qual atribuímos uma reta real e ao valor numérico desta reta real chamaremos de x, daremos o nome de eixo das abscissas. Ao eixo vertical daremos o nome de eixo y ou eixo das ordenadas.
Suponha que este ponto A esteja representado na figura. Trace uma reta paralela ao eixo y e que passe pelo ponto A; o ponto de interseção entre esta reta e o eixo x nós damos o nome de coordenada x do ponto A. Analogamente, trace uma reta paralela ao eixo dos x que passe pelo ponto A; o ponto de interseção entre esta reta e o eixo y é chamada de coordenada y do ponto. Podemos resumir esta informação dizendo que o ponto A possui coordenadas (x;y). Veja a figura a seguir.

No desenho acima podemos dizer que a abscissa do ponto A é igual à 2 e a ordenada é igual à 3 ou, em notação mais compacta, o ponto A possui coordenadas (2;3). Usaremos aqui o ";" para separar x e y, embora há autores, principalmente extrangeiros, que usam ",". Esta opção foi feita para não confundir com o separador usual em português para representar casas decimais. Em inglês, 1,5 (um e meio) é representado como 1.5 (observe a maioria das calculadoras).
À esse ponto podemos sempre associar um segmento orientado que parte sempre do ponto (0;0) e termina em A. Este segmento é equipolente a uma infinidade de outros seguimentos e portanto pode ser usado como representante de um vetor (conjunto). Também é fácil perceber que para todo seguimento orientado de comprimento não nulo, é sempre possível encontrar um seguimento orientado equipolente que parte da origem do sistema de coordenadas e termina em um ponto genérico A (aqui, não nos referimos ao ponto (2;3)). Resumindo: podemos "colocar" todo e qualquer vetor com origem coincidente ao ponto (0;0), inclusive o vetor nulo $\vec{0}$.

Vamos supor que exista um vetor $\vec{x}$ que está representado por um seguimento orientado contido no eixo x. Podemos então escrever um vetor unitário, ao qual daremos o nome de vetor $\hat{i}$ que será definido, conforme visto quando falado de vetor unitário, da seguinte forma: $$|\hat{i}| = \left | \frac{1}{|\vec{x}|} \cdot \vec{x} \right | = \frac{1}{|\vec{x}|} \cdot |\vec{x}| = 1$$ Identicamente, podemos falar em vetor unitário $\hat{j}$ do vetor $\vec{y}$: $$|\hat{j}| = \left | \frac{1}{|\vec{y}|} \cdot \vec{y} \right | = \frac{1}{|\vec{y}|} \cdot |\vec{y}| = 1$$ Posso então dizer que o vetor $\vec{u}$ pode ser obtido somando-se dois vetores perpendiculares entre si sendo um paralelo ao $\vec{x}$ e outro paralelo ao eixo $\vec{y}$.
Na figura a seguir está representado três vetores $\hat{j}$, cujo módulo é unitário, e por isso pode ser colocado entre duas unidades do eixo das ordenadas. No eixo horizontal está representado dois vetores $\hat{i}$.

Observe a seguir uma segunda representação possível para um vetor:

Assim podemos dizer que o vetor $\vec{u}$ é a soma de dois outros vetores: $2\hat{i}$ e $3\hat{j}$. Ou seja: $$\vec{u} = 2\hat{i} + 3\hat{j}$$
Provavelmente você já deve ter tido contato com esta notação. Então daremos mais uma, um pouco mais compacta.
Seja um vetor $\vec{u} = x\hat{i} + y\hat{j}$, ele pode ser representados a seguinte forma: $$\vec{u} = x\hat{i} + y\hat{j} = \left \{ x;y\right \}$$ Aqui usamos as chaves "{" e "}" para não confundir com a representação de ponto (x;y).
Bom, mas sistema coordenado em duas dimensõe não tem graça... Nós vivemos em um mundo de três dimensões espaciais, não é? Então vamos estudar o sistema em três dimensões.
Para isso acrescentemos mais um eixo no nosso sistema de coordenadas. Este novo eixo será o eixo z ou eixo das cotas e localizamos a sua direção fazendo uso da regra da mão direita. Para determinar a direção do eixo z, primeiro escolha as direções dos eixos x e y. Por exemplo, seja o seguinte conjunto de eixos coordenados:

Para isso, abra sua mão deixando todos os seus dedos juntos, com excessão do dedão que deverá apontar numa direção perpendicular aos demais dedos. Aponte com seus dedos na direção do eixo x e gire em direção ao eixo y percorrendo o menor ângulo. A direção de seu dedão irá apontar o eixo z. Observe que na figura acima, o eixo z estará perpendicular ao plano que contem os eixos x e y!
Pratique a regra da mão direita! Ela lhe será extremamente importante!!!

Tradicionalmente usa-se o eixo z na vertical, assim o esquema abaixo é uma alternativa para representar o sistema de eixos coordenados em três dimensões:

Extendendo o conceito de vetores unitarios ligados aos eixos coordenados (estes vetores também são chamados versores), na direção do eixo das cotas temos o vetor unitário $\hat{k}$. Assim podemos escrever qualquer vetor em três dimensões como se segue:

$$\vec{u} = x\hat{i}+y\hat{j}+z\hat{k} = \left \{ x;y;z \right \}$$
Na figura anterior foram omitidas as setas que orientam os eixos x, y e z apenas para evitar confusões futuras. Aproveite também para treinar a "regra da mão direita".
Vamos agora falar dos octantes: a figura abaixo mostra parte dos três planos (que são infinitos) formados pelos três eixos coordenados. Estes três planos dividem o espaço em oito partes tais que para sair de qualquer uma delas e chegar à outra, você deve atravessar algum plano. Nela estão apresentados os "números" para cada octante, isto é, 1 parta o 1$^o$, 2 para o 2$^o$ e assim por diânte. É importante saber a nomenclatura de cada octante para o caso em que os dados que você tem em mãos descrevem seus dados usando estes nomes, mas na física esta nomenclatura será rara, mas mesmo assim vale apena saber, mesmo que somete para problemas específicos (que pode aparecer em questões de matemática).

Introduzida a ideia de plano de coordenada cartesiano, vamos utilizá-lo para descrever algumas figuras mais simples da geometria. Dentre elas, vamos aprender a encontrar a equação de uma reta e de um plano usando vetores. Vamos começar lembrando da equação de distância de ponto à ponto e depois, de forma bem imediata, encontraremos a equação da circunferência e da esfera.
Cabe aqui acrescentar mais um novo assunto: os cossenos diretores.
Observe a figura abaixo. Nela temos um vetor $\vec{v}$ representado em um sistema de eixos cartesianos bem como os ângulos entre cada um dos eixos:




Digamos que você tenha o vetor $\vec{u}$: $$\vec{u}=x\hat{i}+y\hat{j}+z\hat{k}$$
Pode-se calcular os cossenos diretores da seguinte maneira: $$\rm{cos}\alpha = \frac{x}{|\vec{u}|}$$ $$\rm{cos}\beta = \frac{y}{|\vec{u}|}$$ $$\rm{cos}\gamma = \frac{z}{|\vec{u}|}$$
Estes são chamados cossenos diretores e voltaremos a faler deles futuramente.
DISTÂNCIA PONTO À PONTO
São dados dois pontos no espaço, sejam eles os pontos A e B. Se A possui coordenadas ($x_A;y_A;z_A$) e B possui coordenadas ($x_B;y_B;z_B$), qual é a distândia entre os dois pontos?
Para simplificar, vamos primeiramente determinar a distância de um ponto P com coordenadas ($x;y;z$) até a origem do sistema de coordenadas escolhido.
Observe o esquema abaixo.

Pelo Teorema de pitágoras, podemos determinar a distância entre a projeção do ponto P sobre oplano xy e a origem do sistema de coordenadas:

$$c^2=x^2+y^2$$
Entretanto, a distância que queremos encontrar, $d$, pode ser determinada pelo triângulo da figura a seguir:

$$d^2=z^2+c^2$$
Mas sabemos que $c^2=x^2+y^2$, tentão: $$d^2=x^2+y^2+z^2$$
Seguindo este mesmo raciocínio, podemos encontrar a distância entre os pontos A e B. Observe que a equação acima é uma extensão do Teorema de Pitágoras.
Podemos reescrever a equação acima substituindo $x$ por $\Delta x$, $y$ por $\Delta Y$ e $Z$ por $\Delta Z$ para quaisquer dois pontos. Assim pode-se obter que a distância entre os pontos A e B é dada por: $$d_{AB}=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
E assim temos a equação que nos diz a distância entre dois pontos.
EQUAÇÃO DA CIRCUNFERÊNCIA E DA ESFERA
Observe a figura abaixo

Nela temos representado uma circunferência de raio $R$. O que ela tem em comum com o tópico passado: "distância ponto à ponto"?
A resposta é que a circunferência pode ser descrita como sendo o lugar geométrico equidistânte de um ponto, isto é, todos os pontos da figura anterior possuem a mesma distância do cento do nosso sistema de coordenadas.
Assim podemos utilizar o Teorema de Pitágoras para descobrir quais os pontos pertence à circunferência. Vejamos: $$R^2=x^2+y^2$$
Na verdade acabou! É só isso, com a diferênça de que agora $x$ e $y$ são variáveis (ou coordenadas de qualquer ponto contido na circunferência) e não coordenadas de um ponto fixo.
Se pensarmos em uma circunferência com centro não coincidente à origem de nosso sistema de coordenadas, podemos substiruir $x$ por $\Delta x$ e $y$ por $\Delta Y$, para que componham os catetos do triânculo retângulo:

Sendo C = ($x_C;y_C$) o centro da circunferência, então: $$R^2=(\Delta x)^2 + (\Delta y)^2$$ $$R^2=(x-x_C)^2 + (y-y_C)^2$$
Esta é a equação da circunferência.
A equação da esfera é análiga:
Seja uma superfície cujos pontos que a constituem sejam todos equidistantes de um ponto C = ($x_C;y_C$;z_C). Este ponto C é o centro da superfície e a superfície é uma esfera. Seja $R$ o raio desta esfrerae, portanto, a distância de todos os pontos da superfície ao centro C.
Basta aplicar o Teorema de Pitágoras em três dimensões: $$R^2=(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2$$ $$R^2=(x-x_C)^2 + (y-y_C)^2 + (z-z_C)^2$$
Para resumir, temos então que: $$R^2=(x-x_C)^2 + (y-y_C)^2 \text{ é a equação da circunferência}$$ $$R^2=(x-x_C)^2 + (y-y_C)^2 + (z-z_C)^2 \text{ é a equação da esfera}$$
EQUAÇÃO VETORIAL DA RETA
Vamos agora à uma aplicação do uso de vetores: vamos encontrar uma equação vetorial para representarmos uma reta. Mas antes disso, temos que definir o que seria uma soma de um ponto com um vetor. Esta definição entretanto é simples.
Seja um vetor $\vec{v}$ que pode ser representado pelo segmento orientado $\vec{AB}$. Podemos dizer que $$B=A+\vec{v}$$ isto é, estamos somando ao ponto A um vetor $\vec{v}$ e obtendo um segundo ponto B. Pode-se verificar geometricamente que o ponto A é único.
Esta operação possui algumas propriedades, semelhante às dos vetores. São elas:
- $B+\vec{0}=B$
- $B + \vec{u}=B + \vec{v} \Rightarrow \vec{u}=\vec{v}$
- $(P+\vec{u})+\vec{v}=P+(\vec{u}+\vec{v})$
- $A+ \vec{v} =B+\vec{v} \Rightarrow A=B$
- $(P-\vec{v})+\vec{v}=P$
Assim, seja um ponto A ao qual somamos um vetor $\vec{v}$. Encontraremos apenas um ponto B, mas se multiplicarmos o vetor $\vec{v}$ por um escalar $\alpha$ qualquer, encontraremos outro ponto. Chamemos este ponto, resultado da soma, de ponto X. Assim temos:
$$X=A+\alpha \cdot \vec{v} $$Se alterarmos o valor de $\alpha$ livremente, ou seja, se $\alpha$ puder assumir qualquer valor dos números reais, o ponto X irá variar ao longo de uma reta que passa pelo ponto A e é paralela ao vetor $\vec{v}$, ou seja, a equação acima é a equação da reta que contém o ponto A e é paralela ao vetor $\vec{v}$. Observe a figura abaixo na qual há uma animação para representar esta ideia:

Assim, esta é a equação vetorial da reta:
$$\boxed{X=A+\alpha \cdot \vec{v}}$$Exemplo
Encontre a equação da reta que passa pelo ponto $A=(1;0;1)$ e $B=(0;1;0)$.
RESOLUÇÃO:
Observe que o vetor $$\vec{AB}={B_x-A_x;B_y-A_y;B_z-A_z}={⁻1;1;-1}$$ é um vetor paralelo à reta, pois o ponto B é a soma $A+\vec{AB}$. Assim a equação da reta será: $$X=A+\alpha \cdot \vec{v} \Rightarrow$$ $$X=(1;0;1)+\alpha \cdot \left \{-1;1;-1 \right \} \Leftrightarrow$$ $$X=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \}$$ Note que o ponto X é um ponto pertencente à reta e podemos escrevê-lo como sendo $X=(x;y;z)$ em que x, y e z são as coordenadas do ponto X. Assim, podemos reescrever a equação acima e transformá-la em um sistema de equações: $$X=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \} \Leftrightarrow$$ $$(x;y;z)=(1;0;1)+ \left \{-\alpha;\alpha;-\alpha \right \}\Leftrightarrow$$ $$ \left\{\begin{matrix} x & = & 1 & + & \alpha \cdot& \! \! \! \! (-1)\\ y & = & 0 & + & \alpha \cdot & 1\\ z & = & 1 & + & \alpha \cdot & \! \! \! \! (-1) \end{matrix}\right. \Leftrightarrow $$ $$ \boxed{ \left\{\begin{matrix} x & = & 1 & - & \alpha\\ y & = & & & \alpha\\ z & = & 1 & - & \alpha \end{matrix}\right. } $$ Esta é a equação da reta em três dimensões! Como temos um parâmetro (o escalar $\alpha$), esta equação recebe o nome de equação paramétrica.
EQUAÇÃO VETORIAL DO PLANO
Usando a mesma ideia que a anterior, podemos representar a equação de um plano da seguinte forma:
$$\boxed{X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u}}$$Note que a soma dos vetores $\alpha \cdot \vec{v} +\beta \cdot \vec{u}$, em que $\beta$, assim como $\alpha$, é um escalar, nos fornecerá um ponto X pertencente a um plano que é simultaneamente paralelo à $\vec{u}$ e $\vec{v}$ e que contém o ponto A. Assim, variando livremente os escalares $\alpha$ e $\beta$, encontraremos todos os pontos que define um único plano.
Exemplo 1
Determine a equação paramétrica do plano que passa pelos pontos $A=(7;7;1)$ e é paralelo aos vetores $\vec{v}= \left \{1;1;1 \right \} $ e $\vec{u}= \left \{-1;0;1 \right \} $.
RESOLUÇÃO:
Substituindo os dados na equação vetorial do plano teremos: $$X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u} \Leftrightarrow$$ $$(x;y;z)=(7;7;1)+\alpha \cdot \left \{1;1;1 \right \} +\beta \cdot \left \{-1;0;1 \right \} \Leftrightarrow$$ $$(x;y;z)=(7;7;1)+ \left \{\alpha;\alpha;\alpha \right \} + \left \{-\beta;0;\beta \right \} \Leftrightarrow$$ $$ \boxed{ \left\{\begin{matrix} x & = & 7 & + & \alpha & - & \beta \\ y & = & 7 & + & \alpha & \\ z & = & 1 & + & \alpha & + & \beta \end{matrix}\right. }$$
Exemplo 2
Encontre a equação do plano que passa pelo ponto $A=(1;0;1)$ e $B=(0;1;-1)$ e é paralelo ao segmento CD onde $C=(1;2;1)$ e $D=(0;1;0)$.
RESOLUÇÃO:
Primeiro, encontremos dois vetores paralelos ao plano para que possamos usar a equação vetorial do plano: $$\vec{AB}= \left \{-1;1;0 \right \} = \vec{u}$$ $$\vec{CD}= \left \{1;1;1 \right \} = \vec{v}$$
Agora que temos os dois vetores, basta escolher um ponto pertencente ao plano (pode ser A ou B). Escolhendo o ponto A: $$X=A+\alpha \cdot \vec{v} +\beta \cdot \vec{u} \Leftrightarrow$$ $$(x;y;z)=(1;0;1)+\alpha \cdot \left \{-1;1;0 \right \} +\beta \cdot \left \{1;1;1 \right \} \Leftrightarrow$$ $$(x;y;z)=(1;0;1)+ \left \{-\alpha;\alpha;0 \right \} + \left \{\beta;\beta;\beta \right \} \Leftrightarrow$$ $$ \boxed{ \left\{\begin{matrix} x & = & 1 & - & \alpha & + & \beta \\ y & = & & & \alpha & + & \beta \\ z & = & 1 & & & + & \beta \end{matrix}\right. }$$
Exercício
Encontra a equação do plano que contém os ponto A, B e C para cada item a seguir:
a) $A=(1;0;1)$, $B=(2;1;-1)$ e $C=(1;-1;0)$
b) $A=(-1;2;-5)$, $B=(-1;1;3)$ e $C=(3;-1;1)$
c) $A=(-4;4;-12)$, $B=(2;-2;6)$ e $C=(1;-1;3)$. Você chegou em algum resultado estranho? Determine a equação da reta que passa pelos pontos A e B e verifique se é a mesma equação da reta que contém os pontos A e C.
SISTEMA CILÍNDRICO DE COORDENADAS
Vamos agora comentar brevemente sobre outros sintemas de coordenadas.
Até agora nós vimos apenas um, que servirá de base para construir qualquer outra noção de sistema de referencial, inclusive o sistema de coordenadas cilíndrico (ou sistema cilíndrico de coordenadas).
A ideia é tentar localizar um ponto no espaço de coordenadas cartesianas ($x;y;x$) e determinar a posição deste mesmo ponto usando outro sistema. Vamos começar então.
Observe a figura abaixo. Nela está representado um cilindro de raio $s$ e o ângulo $\varphi$. A altura coincide com a cota z do sistema cartesiano e $\varphi$ chama-se ângulo azimutal.

Cada pondo de coordenadas ($x;y;z$) pode ser associado à um ponto de coordenadas ($s;\varphi;z$). O raio $s$ pode variar de zero à $+\infty$, $0 \leqslant \varphi \leqslant 2\pi$ enquanto que $z$ pode ir de $-\infty$ à $+\infty$, como no caso de $z$ no sistema cartesiano. Observe a figura e veja que as relações abaixo são verdadeiras: $$\left\{\begin{matrix} x=s&\rm{cos}\varphi\\ y=s&\rm{sen}\varphi\\ z=z& \end{matrix}\right.$$
Estas relações são na verdade uma maneira de mudar de referencial. Tente isolar o raio $s$ e o ângulo $\varphi$. Se conseguir, terá um conjunto de três equações que mudam do sistema cilíndrico de coordenadas para o sistema cartesiano.
SISTEMA ESFÉRICO DE COORDENADAS
Semelhante ao sistema cilíndrico, o sistema esférico tem como base uma esfera com centro no ponto (0;0;0) e raio $r$. O raio vetor $\vec{r}$ que localiza um ponto qualquer na esfera forma um ângulo $\theta$ com o eixo vertical e a projeção do raio vetor no plano xy forma um ângulo $\varphi$ com o eixo x.

Este é o sistema de referência que se utiliza para localizar um corpo na superfície do planeta Terra se você adotar como eixo z o eixo de rotação da Terra e o polo norte na parte de z positivo. Talvez por esta razão, o ângulo $\theta$ chama-se ângulo polar. O ângulo formado entre a projeção de $\vec{r}$ e o eixo x, $\varphi$, chama-se ângulo azimutal assim como em coordenadas cilíndricas.
A diferença entre as coordenadas geográficas esféricas e as coordenadas esféricas é que nestas últimas, $r$ varia de zero á $\infty$, $0\leq \theta \leq \pi$ e $0\leq \varphi \leq 2\pi$. Já nas coordenadas geográficas, $r$ é o raio da Terra (aproximadamente constante); o ângulo polar é substituído por outro (latitudinal) que é medido a partir da linha do equador indo de zero (na linha do equador) até $+\pi/2$ no polo norte e de zero à $-\pi/2$ no polo sul; por fim o ângulo equivalente ao azimutal é o longitudinal que tem como zero o meridiano que passa na Inglaterra na cidade de Greenwich e varia de zero a $+\pi$ na direção leste e de zero a $-\pi$ na direção oeste.
Verifique as equações a seguir de transformação de sistema de coordenadas: $$ \left\{\begin{matrix} x=r&\rm{sen}\theta&\rm{cos}\varphi\\ y=r&\rm{sen}\theta&\rm{sen}\varphi\\ z=r&\rm{cos}\theta \end{matrix}\right.$$
CENTRO DE MASSA
Centro de massa está intimamente ligado ao conceito de centro de gravidade e, por hora, consideraremos ambos como sendo sinônimos (eles são diferentes e ficará mais claro o conceito de centro de massa quando estudar gravitação universal; já centro de gravidade é mais intuitivo). Vamos então tentar entender, de forma mais ou menos intuitiva, o que é centro de gravidade.
Imagine que você queira pendurar uma vassoura de piaçava utilizando um barbante. Onde você deve prender o barbante? Certamente mais próximo às fibras de piaçava que da ponta do cabo e a resposta mais intuitiva é que "a região com as fibras são mais 'pesadas' que o cabo". Vamos dizer diferente: divida a vassoura no meio deixando puco mais da metade do cabo de um lado e o restante do outro. Na verdade a parte com as fibras de piaçava possuem mais massa! Assim você deve amarra a vassoura em algum ponto mais próximo das fibras.
Considere um ponto A de coordenadas ($x_A;y_A;z_A$) e B de coordenadas ($x_B;y_B;z_B$). Coloquemos um corpo muito pequeno (que chamaremos de corpo pontual) de massa $m_A$ em A e um corpo pontual de massa $m_B$ em B. O centro de massa (ou, mais intuitivamente, caso ambos os corpos estivessem presos por uma haste muito leva, o ponto onde deveríamos prender a haste para permanecer em equilíbrio) é dado por: $$CM_1=\frac{m_AA+m_BB}{m_A+m_B}$$ Entenda que estamos trabalhando com pontos.
Se colocarmos uma terceira massa $m_C$ em um ponto $C=(x_C;y_C;z_C)$, teríamos: $$CM_2=\frac{(m_A+m_B)CM_1+m_CC}{(m_A+m_B)+m_C}\Rightarrow $$ $$CM_2=\frac{(m_A+m_B)\frac{m_AA+m_BB}{m_A+m_B}+m_CC}{m_A+m_B+m_C}\Rightarrow $$ $$CM_2=\frac{m_AA+m_BB+m_CC}{m_A+m_B+m_C}$$
Assim, se escolhermos $n$ pontos, $P_1$ e nele colocarmos uma massa $m_1$, $P_2$ e nele colocarmos uma massa $m_2$, $P_3$ e nele colocarmos uma massa $m_3$, e assim até o n-ésimo ponto $P_n$ com massa $m_n$ teríamos como centro de massa $CM$ o ponto assim calculado: $$ CM=\frac{\sum_{i=1}^{n} m_iP_i}{ \sum_{i=1}^{n} m_i}$$
É importante observar que acima temos uma notação compacta e que o ponto $CM$ na verdade é o ponto ($x_{CM};y_{CM};z_{CM}$) e a equação para as coordenadas ficaria como se segue: $$ \left\{\begin{matrix} x_{CM}=\frac{\sum_{i=1}^{n} m_ix_i}{ \sum_{i=1}^{n} m_i}\\ y_{CM}=\frac{\sum_{i=1}^{n} m_iy_i}{ \sum_{i=1}^{n} m_i}\\ z_{CM}=\frac{\sum_{i=1}^{n} m_iz_i}{ \sum_{i=1}^{n} m_i} \end{matrix}\right.$$
Como um exemplo, vamos mostrar que se tivermos três pontos A, B e C não alinhados em cada um um objeto pontual de massa $m$. Se traçarmos uma linha de um dos pontos (por exemplo, o ponto A) passando pelo centro de massa dos outros dois (isto é, pelo ponto médio), o centro de gravidade se encontrará a uma distância $x$ do ponto médio de B e C e $2x$ do ponto A.

Na verdade a solução é bem simples. Primeiramente, você não precisa se ater aos sistemas de coordenas, pois o que as equações acima nos mostra é que as massas atuam como uma média ponderada. Então, pense em um eixo coincidente com a reta que traçamos (chamada de bissetriz) e chame de $y$ a distância do centro de massa $CM$ até o ponto A e de $x$ a distância entre $CM$ e o ponto médio do segmento BC. Adote como sendo 0 (zero) o valor da coordenada do $CM$. Então: $$CM=\frac{2mx+my}{2m+1m}\Rightarrow $$ $$0=\frac{2x+y}{3}\Rightarrow $$ $$0=2x+y\Rightarrow $$ $$y=-2x$$ Observe que o sinal negativo se deve por termos escolhido como origem o ponto $CM$, assim se $Y$ for positivo, $x$ é negativo, e vice-versa.
DEMONSTRAÇÃO DA LEI DOS COSSENOS
Vamos à uma breve demonstração da lei dos cossenos. Para isso, seja um vetor $\vec{u}$ e um vetor $\vec{v}$ quaisquer, representados na figura a seguir.

Podemos escolher um referencial qualquer para representarmos estes dois vetores em termos de suas coordenadas. Escolheremos então um referencial no qual o vetor $\vec{u}$ esteja contido no eixo x. Assim, em termos de suas coordenadas e baseado na figura abaixo, teremos:
 $$\left \{
\begin{matrix}
\vec{u} & = & u\cdot \hat{i}&\\
\vec{v} & = & v\cdot \rm{cos}\theta\cdot\hat{i} &+ &v \cdot \rm{sen}\theta\cdot\hat{j}
\end{matrix}\right.$$
$$\left \{
\begin{matrix}
\vec{u} & = & u\cdot \hat{i}&\\
\vec{v} & = & v\cdot \rm{cos}\theta\cdot\hat{i} &+ &v \cdot \rm{sen}\theta\cdot\hat{j}
\end{matrix}\right.$$
A soma $\vec{S}$ desses vetores será dada por:
$$ \vec{S}=\vec{u}+\vec{v}=(u+v\cdot cos\theta) \cdot\hat{i} + v \cdot sen \theta\cdot\hat{j} $$O módulo ao quadrado da soma ($|\vec{S}|^2$ ou $S^2$) pode ser determinado:
$$ |\vec{S}|^2=(u+v\cdot cos \theta)^2 + ( v \cdot sen\theta)^2 \Leftrightarrow $$ $$ S^2=u^2+2uv\cdot cos\theta+ v^2\cdot cos^2\theta + v^2 \cdot sen^2\theta \Leftrightarrow $$ $$ S^2=u^2+2uv\cdot cos\theta+ v ^2(cos^2\theta +sen^2 \theta)\Leftrightarrow $$ $$ \boxed{S^2=u^2+ v ^2+2uv\cdot cos\theta} \; \; \; \; \; \; \; \boxed{} $$DEMONSTRAÇÃO DA LEI DOS SENOS
A lei dos senos pode ser demonstrada rapidamente utilizando-se um triângulo qualquer. Como queremos uma aplicação vetorial, comecemos com o triângulo a seguir cujos lados estão representados os vetores $\vec{u}$, $\vec{v}$ e $\vec{w}$, cujos módulos são, respectivamente, $u$, $v$ e $w$ e representam os lados do triângulo, que chamaremos simplesmente de lados $u$, $v$ e $w$.

Observe que a altura do triângulo em relação ao lado $w$ é:
$$ u\cdot sen\beta=v \cdot sen\alpha $$A altura em relação à $v$ será:
$$ u\cdot sen\delta=w \cdot sen\alpha $$Por fim, a altura em relação à $u$ será:
$$ w\cdot sen\beta=v \cdot sen\delta $$Essas três equações podem ser reescrita conforme se segue:
$$ \left\{\begin{matrix} \frac{u}{sen\alpha} & = & \frac{v}{sen\beta}\\ \frac{u}{sen\alpha} & = &\frac{w}{sen\delta} \\ \frac{w}{sen\delta}& = &\frac{v}{sen\beta} \end{matrix}\right. $$A partir deste sistema, a lei dos senos é imediata
| $$ \frac{u}{sen\alpha} = \frac{v}{sen\beta}= \frac{w}{sen\delta} \; \; \; \; \; \boxed{} $$ |
BIBLIOGRAFIA
- Paulo Boulos, Ivan de Camargo, GEOMETRIA ANALÍTICA UM TRATAMENTO VETORIAL, 3$^a$ ed., pp. 1 - 17.