LISTA DE CONTEÚDO
- Introdução à dilatação térmica
- Dilatação linear
- Dilatação superficial
- Dilatação volumétrica
- Exercícios
- Bibliografia
INTRODUÇÃO À DILATAÇÃO TÉRMICA
Vamos começar agora a tratar de um novo tema: a dilatação térmica. Se você encontrou esta página em uma bisca na internet, recomendo que você veja a aula anterior clicando aqui, pois farei referências a assuntos abordados lá.
Como visto na aula anterior, a temperatura de um corpo está relacionada à energia cinética dos átomos e moléculas do corpo em estudo. Anteriormente discutimos este fato apenas com relação aos sólidos, mas agora iremos inserir os líquidos nesta ideia.
Comecemos com a figura usada na aula anterior, que representa os átomos e moléculas como pequenos círculos e as internações entre eles(as) como advindas de molas pequenina.
Embora tenhamos visto este esquema para representar corpos sólidos, podemos estender esta ideia/representação para líquidos tomando o seguinte cuidado: seja um átomo quaisquer que chamaremos de átomo A, quando pensamos em um sólido é razoável supor que os átomos que mais interagirão com o átomo A serão os átomos mais próximo deste, ou seja, os átomos que estão ligados por estas molas fictícias à A; enquanto um átomo está fortemente ligado aos demais átomos que constitui o corpo sólido, isto não é verdade para líquidos, onde átomos um pouco mais distântes também interagem com o átomo escolhido.
Basicamente a maior diferênça entre um sistema sólido e um líquido é a força entre os átomos (na verdade, na maioria dos casos são moléculas e a força é inter molecular) e a mobilidade, pois um átomo (molécula) de um líquido pode transitar entre os demais átomo (molécular).
Imagine agora que aquecemos este sistema: como já discutido anteriormente, aumentar a temperatura consiste em aumentar a vibração das molécular, pois temperatura se relaciona à velocidade. Acredito que deve ser fácil imaginar que quando estas moléculas começam a vibrar mais, em média elas ficarão mais distantes entre si, assim o volume total do seu material irá aumentar. Uma analogia que pode ser feita aqui é a seguinte: imagine que você vá a algum show no qual a banda começa a tocar uma música tranquila; na pista as pessoas quase não se agitam, ficando próximas umas das outras; subtamente, a banda começa a tocar um "rock pauleira" e um grupo de fãs começam a pular loucamente. Você deve imaginar que este grupo irá "se expandir", ocupando uma área maior que a inicial. É isso o que acontece com os átomos (e molécular) de um corpo quando se aumenta a temperatura do corpo: as moléculas se agitam e aumentam o tamanho de suas fronteiras.
DILATAÇÃO LINEAR
Podemos começar o estudo quantitativo da dilatação supondo que temos uma barra longa, feita por exemplo de metal. Mas o que significa ser longa? Significa que as demais dimensões da barra serão desprexíveis com relação ao comprimento.
Vamos tentar entender a relação entre a variação do comprimento da barra, que chamaremos de $\Delta L$, com o comprimento inicial $L_o$ da barra e a variação de temperatura ($\Delta T = T-T_o$ em que $T$ é a temperatura final da barra após o aquecimento e $T_o$ é a temperatura inicial).
Já sabemos que o comprimento da barra será tanto maior quanto maior a temperatura, assim $\Delta L$ é proporcional à $\Delta T$. É razoável supor que $\Delta L$ também seja proporcional ao comprimento inicial, pois barras pequenas devem aumentar seu comprimento menos que barras grandes
Podemos dizer então que: $$\Delta L \propto L_o \cdot \Delta T$$ sendo o símbolo $\propto$ chamado símbolo de proporção direta ou simbolo de proporção direta, que significa que as grandezas à esquerda se $\propto$ são proporcionais às grandezas da direita, porém não é garantida a igualdade. Aqui leia-se: "delta éle é proporcional à éle zero vezes delta tê". Cuidado aqui, pois o símbolo de proprcionalidade $\propto$ é diferente da letra grega alfa $\alpha$.
Relembrando o exemplo do show no qual um grupo de pessoas começou a pular loucamente, podemos imaginar que outro grupo de pessoas, no mesmo show, possa se empolgar menos e dançar menos. Da mesma forma é razoável supormos que para cada material que constituir a barra anterior, teremos uma variação do comprimento diferente. De fato, o aço, por exemplo, dilata mais que o vidro: se pegarmos duas barras delgadas de mesmas dimensões, porém uma de aço e outra de vidro, a de vidro irá dilatar mais. Supondo então que a relação de proporcionalidade acima seja verdadeira e chamando de $\alpha$ o número de proporcionalidade que devemos utilizar m nesta relação, mas que depende do material que estiver sendo usado. Assim: $$\boxed{\Delta L = L_o\cdot \alpha \cdot \Delta T}$$
De fato esta equação tem uma ótima aplicabilidade do ponto de vista experimental, isto é, o comportamento do comprimento de barras delgas é bem descrito por esta equação.
Aqui, gostaria de sugerir que memorize bem esta equação e o que ela significa, pois todas as demais equações a seguir serão consequências diretas desta equação ou será resultado de uma análise semelhante.
Lembrando que tudo que é "$\Delta$" na física costuma ser final menos o inicial e seja $L$ o comprimento final da barra, podemos obter: $$\Delta L = L_o\cdot \alpha \cdot \Delta T \Leftrightarrow L-L_o=L_o \cdot \alpha \cdot \Delta T \Leftrightarrow $$ $$ L=L_o+L_o \cdot \alpha \cdot \Delta T \Leftrightarrow $$ $$ \boxed {L=L_o(1+\alpha \cdot \Delta T)} $$ O gráfico desta equação será uma reta:
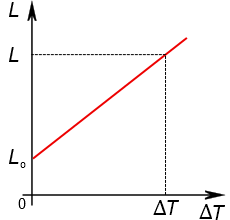
Observe que a equação anterior é na verdade a equação de uma reta. Comparando a equação $ L=L_o+L_o \cdot \alpha \cdot \Delta T$ com a equação da reta $y=b+ax$, pode-se perceber que o coeficiente angular será $L_o \cdot \alpha$. Assim, digamos que seja apresentado um gráfico que expressa o comprimento de duas barras em função da variação da temperatura, como apresentado na figura a seguir:
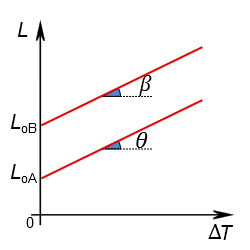
Vamos comparar então o coeficiente de dilatação térmica destes dois objetos. Para começar, sabemos pelo gráfico que $L_{oB}>L_{oA}$. Agora devemos saber qual dos dois gráficos possui maior coeficiente angular, isto é, $tan \theta$ e $tan \beta$.
No primeiro caso, supondo que $tan \theta > tan \beta$, teremos que $L_{oA} \cdot \alpha_A > L_{oB} \cdot \alpha_B$. Como $ L_{oA} < L_{oB} $, então devemos ter que $ \boxed { \alpha_A > \alpha_B } $.
No segundo caso, seja $ tan \theta = tan \beta $, então $L_{oA} \cdot \alpha_A = L_{oB} \cdot \alpha_B$. Como $ L_{oA} < L_{oB} $, então devemos ter que $ \boxed { \alpha_A < \alpha_B } $. Note que isto faz sentido, pois como ambos dilatam da mesma quantidade para uma mesma variação de temperatura, é necessário que a barra inicialmente mais curta dilate proporcionalmente mais que a barra inicialmente mais longa.
Em último caso, quando $tan \theta < tan \beta$, teremos que $L_{oA} \cdot \alpha_A < L_{oB} \cdot \alpha_B$. Como $ L_{oA} < L_{oB} $, nada poderemos afirmar pois é possível que $ \alpha_A > \alpha_B $ satisfaça as condições apresentadas assim como $ \alpha_A < \alpha_B $ pode também satisfazer.
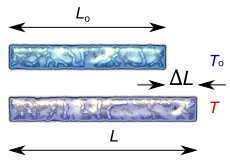
Para ilustrar o que estamos tratando aqui, observe a figura abaixo na qual temos uma barra delgada com comprimento inicial $L_o$, foi aquecida de uma temperatura inicial $T_o$ até uma temperatura final $T$ sofrendo uma variação de comprimento $ \Delta L = L - L_o $:
DILATAÇÃO SUPERFICIAL
Quando falamos em dilatação linear estamos imaginando uma barra delgada cujo comprimento possui dimensão muito maior que qualquer outra (por exemplo, o raio da base da barra é muito menor que o comprimento da barra), ou seja, disprezamos qualquer dilatação nas outras duas direções.
Vamos agora tratar de dilatação de área. Para isso, imagine um retângulo de lados $L_{o1}$ e $L_{o2}$